引言

　　LabWindows/CVI美國國家儀器公司(NI公司)推出的交互式C語言開發環境。LabWindows/CVI以ANSIC為核心，將功能強大、使用靈活的C語言與用于數據采集分析和顯示的測控專業工具有機地結合起來。它的集成化開發環境、交互式編程方法、函數面板和豐富的庫函數大大增強了C語言的功能，為熟悉C語言的開發人員建立了檢測系統、自動測試環境、數據采集系統、過程監控系統、虛擬儀器等提供了一個軟件開發平臺。Matlab是由Math Works公司于1984年推出的一套科學計算軟件。它具有強大的矩陣計算和數據可視化能力，一方面可以實現數值分析、優化、統計、偏微分方程數值解等若干個領域的數學計算;另一方面可以實現二維、三維圖形繪制，圖像處理、虛擬現實等方面的處理。

　　本文的出發點是利用Matlab強大的數學處理功能，對某平臺高頻測試功率衰減問題進行數據分析，并以此建立高頻通道功率衰減數學模型。并在此基礎上采用LabWindows/CVI這一軟件開發平臺，利用其靈活豐富的庫函數，以及可以輕松實現數據分析和顯示的軟面板功能來控制測試儀器，在獲取儀器測試實際數據的基礎上，將測試得到高頻信號頻率帶入建立的衰減數學模型進行計算得到此時的功率衰減值，并將此數值與實際測得功率值相加顯示到虛擬儀器面板上，作為最終的測試結果。從而實現了編程環境中C語言的高效執行效率和科學計算相結合的目的，試驗證明了該方法的有效性。

　　1 通用ATS傳輸通道結構分析

　　ATS硬件結構和接口電路設計具有一定的共性，其一般測試結構如圖1所示，從圖中可以看出實現信號傳輸的通道結構主要包括2個部分：一是ATE(Auto Test Equipment，自動測試設備)中信號流經的途徑，一般流程部件為測試儀器-連接線纜-開關-連接器;二是適配器結構，根據UUT測試需求實現開關系統的靈活配置，以及完成信號調理。適配器設計一方面存在功能上的共性，即需要完成放大、衰減、濾波、隔離、線性化等信號調理功能;另一方面也有其特殊性，如必須結合UUT具體測試要求，設計各種調理電路。而ATE在設計完成后，具有結構功能不變性，特別對高頻信號而言，其本身特點不能按一般的集總系統理解，故此需要對這一特定的信號傳輸特性進行分析。

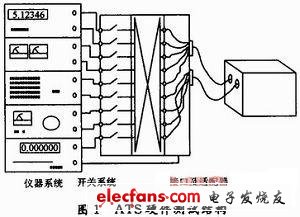
　　ATE中測試高頻信號主要關注其頻率和功率2個參數，經過試驗已證實，高頻信號經過傳輸通道(電纜、開關、連接器)時對頻率測試精度影響很小，可以忽略;而信號的功率會隨著頻率的改變而有規律的變化。這種衰減產生的原因包括以下幾個方面：

　　(1)電纜在傳輸信號時會產生趨膚效應損耗和介電損耗。其中高頻信號沿著導體內側的表面傳輸，這種現象即為所謂的趨膚效應;絕緣材料在電場作用下，由于介質電導和介質極化的滯后效應，在內部引起的能量損耗，由于電介質絕緣體會影響電纜的電容，電介質絕緣體同樣會產生與頻率相關的電纜損耗，即介質損耗。在自動測試設備中，介電損效應是高頻信號產生損耗的主要原因。

　　(2)開關和連接器作為特殊的連接線，同樣會使信號傳輸時產生衰減。

　　(3)這些元件連接到一起后，由于阻抗不完全匹配會引起信號波反射，產生反射損耗，并且元件之間焊接處不可避免地會產生頻譜泄漏等，都將導致信號功率衰減。對于前2種功率損耗，電纜、開關和連接器在出廠時都給出了不同頻率段下功率衰減值，而對于第3種因素產生的損耗，是不可預知的，需要在完成設計后進行測定。

　　另外，上述幾種元件使用時，因其老化和溫度變化不可避免的會產生隨機誤差，如連接器的本振頻率會隨著溫度變化產生漂移等。因此，為減小這些隨機誤差，一方面應選擇高質量的元件;另一方面要定期對ATE進行計量，以便及時調整相關測試參數。

　　2 基于Matlab建立高頻傳輸衰減模型

　　2.1 獲取高頻信號傳輸通道功率衰減值

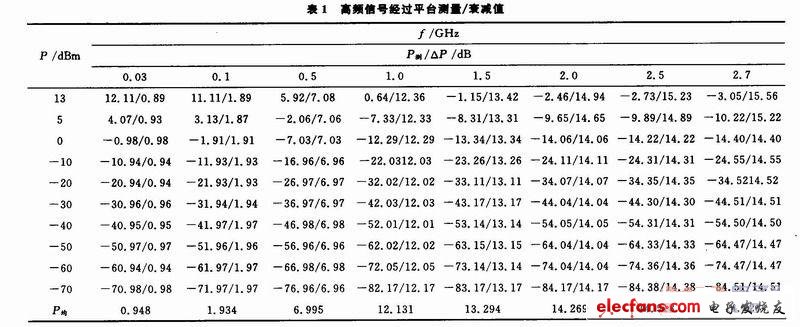
　　本文旨在結合Matlab和LabWindows/CVI兩者的優勢，為ATS中高頻通道傳輸損耗設計一種軟件補償的方法。功率衰減與其大小無關，而是隨頻率改變而變化，本文以某平臺為基礎，對頻率范圍在[30 MHz，2.7 GHz]內的高頻信號源進行測試，得到(不同頻率、功率)信號經過傳輸通道的功率衰減值，如表1所示。

　　2.2 高頻信號傳輸通道功率衰減建模

　　在測量數據處理中，常常遇到根據測量數據確定給定模型的參數;為離散測量數據建立連續模型2類問題。本文的數據處理工作屬于第2種，在這類問題的測量數據處理方法中，比較好的是選取能夠描述測量數據特征的某類曲線，在一定意義下從這類曲線中尋求一條“最好”的曲線作為實驗數據對應的連續模型，并給出該連續模型對應的參數。這種處理思想被稱為“擬合”，本文將采用經典的最小二乘擬合方法進行數據處理。

　　2.2.1 最小二乘擬合

　　以兩元模型為例，假設x和y分別為測量數據矢量，x*和y*分別為對應的真值矢量，f為擬合模型，θ為模型參數矢量，則：

　　由式(2)列出對應的正規方程并求解就可以得出模型參數的最小二乘估計值。最小二乘擬合的理論基礎是高斯-馬爾可夫定理，其發展已有約兩百年的歷史，在數據處理中被廣泛應用。最小二乘估計具有無偏性和方差最小的性質，且與測量矢量所服從的概率分布無關，因而當測量矢量的概率分布形式不能嚴格知道，無法使用經典統計中的參數估計理論時，最小二乘擬合成為了數據處理的一種簡便方法，同時這也是最小二乘擬合在數據處理中被廣泛使用的原因。基于上述原因，本文選取最小二乘擬合方法對測試數據進行處理。