幀的gDACtionPointOffset是全局參數，但是由于TSS截短的影響，同步幀接收節點見到的TSS的1/0跳變沿的時間與接收節點ActionPointOffset時間之差并不是節點的時鐘差，所以它用第一個BSS中的1/0跳變沿來倒推發送節點ActionPointOffset，如圖1所示。倒推是該時刻減去常數pDecodingCorrection和pDelayCompensation得到發送節點TSS的開始時刻。PDecodingCorrection內含有TSS、FSS、BSS、總線濾波延遲和位采樣延遲各項。pDelayCompensation內含有收發器延遲、星型耦合器延遲和電纜長度的傳輸延遲。pDelayCompensation的數值取簇中的最小者。由此倒推出的發送節點的動作點稱為primaryTRP,發送和接收的節的動作點的時間偏差就被記錄下來。

　　接收節點對每一個同步幀都加記錄，該同步幀接收是否正確也記錄在案。只有接收正確的偏差才能用于校正計算之中。

　　FlexRay有相位與頻率的校正，為了頻率校正，需要連續2個cycle的同一同步節點所發的幀的偏差，所以校正是以2個cycle為周期進行的。頻率校正的計算結果在每個奇數cycle內完成，下一個cycle開始生效，在MT形成過程中實行，因此是均勻分布的。相位校正在奇數cycle的末尾完成，在該cycle的網絡空閑段實行。

　　4 FlexRay算法的問題

　　圖2 同步節點位置分布舉例

　　時鐘偏差推算是造成飄移的原因。圖2中有4個同步幀發送節點1～4，各相距8 m，節點5是普通非同步幀發送節點。按規定，pDelayCompensation是一個預定的常數，該按最小值選取，對圖2的情況，就是節點5和節點2間的延遲，即接近為0。這樣，對實際發生的延遲是補償不足的。不足部分可寫為：

　　節點間的延遲，按每米10 ns計，最大距離為24 m，那么此補償不足量有0.24 μs。

　　在圖1中，假定同步幀在cycle的第一個static slot，對static slot的開始時間有一個標準的參考點，發送節點和接收節點各有相位差TT(0)和TR(0)，此時接收節點得到的偏差將含有延遲補償不足的部分：

　　由于距離不同，接收節點得到的URT也是不同的。

　　FlexRay規定，發同步幀的節點在屬于自己的slot上的相位誤差登記為0。假定節點間原來已處于接近同步的情況，對節點1而言，e11=0最小，e14最大，按算法它們將被丟棄，于是校正量將按(e12+ e13)/2計算：

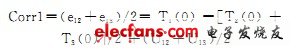
　　當節點初始相位比參考節點2、3的平均相位早時，應該推遲本節點下一cycle的開始，實現負反饋。就應有T1(1)= T1(0)-Corr1。為了分析問題的需要，假定只作一部分校正，即：

　　其中系數c≤1，對FlexRay而言c=1。于是有：

　　推而廣之，將各節點的相位差寫為向量，可以得到狀態方程：

　　對T1而言，系數a11=1-c，a12= c/2，a13= c/2，a14=0，B=-c，U1=120 ns。對節點2而言，它丟棄最大的e24和最小的e22，U2=80 ns。類似可確定其他節點的系數。所以矩陣A有：

　　同時有B=-c和U=[120ns 80ns 80ns 120ns]T(6)

　　對A求取特征根得到：λ1=1，λ2= 1-c，λ3=λ4=1-1.5c。

　　然而在FlexRay中URT是一個系統性偏差，并不因一次校正而消失，因此按(4)式工作時時鐘差會不斷移動。當U不變時有：

　　令(7)式中的第二項為S，則有：

　　(8)式右邊各項均為有限值，而因為A的特征根有λ1=1，(I-A)是不可求逆的，所以S將含有不定值，所以隨著n的增加， T(n+1)是不斷漂移的。