人工智能和數學變換用于電能質量的研究綜述
近年來,由于故障、動態運行和非線性負荷的加入,使動態電能質量問題越來越復雜,因此電能質量的問題重新受到關注。特別是隨著小波理論自身的發展和世界范圍內小波分析算法研究熱潮的興起,以及各種人工智能技術在電力系統的成功應用,對動態電能質量擾動的起因和來源有了很好的理解,對動態電能質量的識別、檢測、分類和統計有了很 好的解決辦法。為了在現有研究成果的基礎上,進一步對動態電能質量進行研究,明確尚需進行的工作,在大量查閱各種國際會議、學術刊物上發表的電能質量論文后,本文綜述了近年來人工智能和傅立葉變換、短窗傅立葉變換和小波變換在電力系統電能質量評估應用中的主要成果與方法,并提出若干需要解決的問題,已資拋磚引玉。
??? 關鍵詞: 傅立葉變換;小波變換;人工智能;動態電能質量
A summary of AI & mathematics transform applied to power quality study?
Wang Jing1, Shu Hong-chun2, Chen Xue-yun1
(1 Harbin Institute of Technology,Harbin,150001)
(2 Kunming University of Science and Technology, Kunming, 650001)?
??? Abstract: In the past decade, faults, dynamic operations, or nonlinear loads make the dynamic Power Quality complex. Thereby, increasing interest in power quality has evolved. With the development of wavelet theory, worldwide spread on the study of wavelet algorithm and the success applications of various AI techniques in power system, the causes and origins of dynamic power quality have a better comprehension. Meanwhile, the solutions of detection, identification, classification and statistics to power quality have been largely improved. In order to propel the further study on the power quality and realize the researches needed done, the main achievements and methods of power quality study, including AI, Fourier transform, Short-time Fourier transform, Wavelet transform, are surveyed in this paper after consulting lots of PQ thesises in conferences and science periodicals. Literature also exposes certain problems to be solved.?
??? Keywords: Fourier transform, wavelet transform, AI, dynamic power quality
0? 引言
??? 電能質量的概念自從提出以來就一直含糊不清,用戶方、制造方和供電方對之的理解也大相徑庭。早期用戶設備對電壓擾動不敏感,而且不容易對系統電壓與頻率造成負面影響,因此用電壓和頻率的偏移或畸變程度來衡量電能質量的好壞就足夠了。近年來,由于以下原因,電能質量問題變得復雜起來:1)電力電子設備和敏感的微處理控制器的使用;2)工業處理過程的復雜化;3)大型計算機的投入;4)用于提高電力系統穩定性的FACTS裝置的大量運用;5)高效可調速電動機等電力設備的投切;6)龐大的電網互聯結構;7)生產精密設備的要求。因此,傳統的電能質量的概念被IEEE第22標準協調委員會推薦采用的11種動態電能質量專用術語[1]取代:斷電(Interruptions)、頻率偏差(Frequency Deviations)、電壓跌落(Sags)、電壓上升(Swells)、瞬時脈沖或突波(Transients Surges)、電壓波動(Voltage Fluctuations)、電壓切痕(Notches)、諧波(Harmonics)、間諧波(Interharmonics)、過電壓(Overvoltages)和欠電壓(Undervoltages)。隨之而來的問題是缺乏對這些暫態現象行之有效的檢測分析方法。只有正確識別影響電能質量的諸多因素、查明相應的起因和來源、檢測、分類并統計擾動現象、確定擾動范圍和幅值才能從根本上綜合治理并提高系統電能質量。
??? 為此,國際上以多種形式、用各種方法和技術對電能質量的擾動問題展開了多方面的研究與探討。綜合起來,這些方法可以歸為利用各種數學變換、利用各種人工智能技術,以及利用人工智能和數學變換結合的方法對擾動進行檢測、分類和抑制。?
1? 數學變換的應用
1.1 傅立葉變換
??? 影響電能質量的暫態信號通常具有很寬的頻譜,將其按頻譜展開能揭示故障的本質。傅立葉變換(FT)就是最常見的一種將時域特征和頻域特征聯系起來的工具。通過傅立葉變換可以提供平穩信號所含諧波的次數、各次諧波的幅值及其初相角并以幅頻特性的形式表現出來,因此可以用于提取由于變壓器、交直流換流設備等造成的周期性諧波分量[2-4]。FT的缺點是:1)必須獲得信號在時域中的全部信息;2)對信號的局部畸變沒有標定和度量能力,因此無法充分描述時變非平穩信號的特征; 3)無法反映信號在局部時間范圍內和局部頻帶上的譜信息。
??? 解決的一個辦法是短時傅立葉變換(STFT),通過引入一個滑動的時間局部化“窗口函數”,對信號進行分段截取,從而得到信號在某一固定時窗和頻窗內的局部時-頻信息。選擇相對于擾動小的多的時窗(必須仔細選擇時窗以避免吉布斯現象),STFT可以很好地反映信號局部范圍內的諧波次數及幅值[5-7], 因此適用于檢測與諧波相關的擾動。STFT的缺點是:1)沒有離散正交基,因此在進行數值計算時沒有象FFT這樣有效的快速算法;2)一旦選定窗口函數,時-頻窗的窗口形狀是固定的,所以對非平穩信號的分析能力有限,盡管文獻[6]提出用寬時窗和窄時窗分別對信號進行掃描,但仍無法改變STFT單一分辨率的事實。
??? 用Wigner譜分析方法可以克服STFT的上述缺點,它是基于兩個信號內積的傅立葉變換,和STFT一樣是時-頻二維聯合分布函數,可以近似看作在時-頻二維平面上的能量密度函數。由于它具有較高的分辨率、能量集中性和跟蹤瞬時頻率的能力,用于進行電能質量分析時,不但可以準確測量基波和諧波分量的幅值,而且能夠準確檢測到信號發生尖銳變化的時刻[5,8,9]。它的不足在于:1)必須以大于Nyquist采樣頻率兩倍以上的頻率進行采樣;2)存在嚴重的交叉干擾現象。
1.2 小波變換
??? 國外最早關于小波變換在電力系統中的應用的文章就是針對電能質量的評估展開的[10]。國內期刊上首次出現這方面的文章介紹則是在1999年[11],而到目前為止,在這方面所開展的工作仍然很少。
1.2.1 擾動的識別
??? 利用小波變換在突變點的特性,可實現對電能質量中的周期性陷波、暫態振蕩、電壓跌落以及閃變等擾動問題的幅值、發生時間與持續時間等特征參數的判斷。1994年,S.Santoso首先在文獻[12]提出小波變換是評估電能質量的有效方法。該文用db4和db10小波函數分別對電壓跌落、平頂波和諧波畸變進行小波變換,實現了對電能質量擾動的檢測與時間定位。但并未討論小波母函數的選擇對檢測結果的影響。文獻[13]則通過分析比較得出db4小波是db小波系中最適用于檢測電能質量擾動的小波的結論。文獻[14]還對重構信號和原始信號的誤差以及小波分析和傅氏分析的結果進行比較。另外,利用連續小波變換后的時-頻相平面圖可檢測電壓跌落和瞬時過電壓[15];利用小波變換的模極大值理論[16-18]同樣可精確地對電壓跌落的發生、恢復時刻進行定位。文獻[19]則傾向于對傅氏變換和小波變換下電壓下降的三個指標:RMS、最大值和基頻幅值進行比較,該文同時還分析了不同時窗選擇的重要性。
??? 為了提取暫態信號中各分量的幅值包絡、相位、瞬時頻率等特征信息,得到比實小波更多的信息,可采用基于小波變換的解析信號分解方法[20],或以復小波為小波母函數[21-22],利用復小波變換的復合信息和相位信息輔助幅值信息進行擾動信息檢測。
1.2.2 擾動數據的壓縮
??? 當電力系統發生擾動后,為了記錄下完整的擾動信息,通常需要1~4MHz的采樣率,使得數據量極大。如此龐大的數據量向調度中心上傳時,不但占用數據通道時間過長而且容易造成數據通道阻塞。這使電磁暫態信號的數據存儲和數據通信均面臨如何提取暫態信號中的有效部分,實現數據壓縮的挑戰。電力系統中現有擾動監測儀的數據簡約技術采用重疊方法即對現有數據不斷覆蓋,或采用量化技術即把一系列相同的波形看成一個整體[23]。這兩種方法的確節省了存儲空間,但卻不是一般意義上的數據壓縮概念。利用小波變換分解和重構的特性對電壓擾動數據進行壓縮[24-27]的算法見圖1。該方法首先定一個閾值,然后將絕對值小于閾值的信號的小波變換系數置為零,僅僅將非零系數的位置及 其數值記錄下來。這種方法的壓縮比主要決定于非零系數的多少,一般壓縮后的數據長度只有原信號的1/6-1/3,相應的壓縮率可達到3-6倍。將壓縮后的信號重構所得到的恢復信號與原始信號的歸一化均方誤差小于10-6-10-5。這樣經過壓縮既節省了錄波器內存又節約信道,且壓縮造成的失真小。
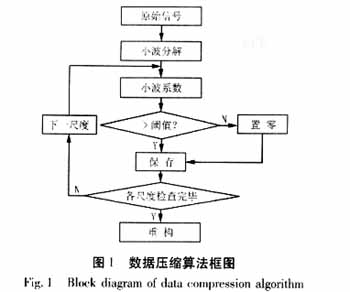
1.2.3 擾動的分類
??? 文獻[28]是最早以文章的形式發表的運用小波理論對擾動進行分類的文章。該文運用一非正交的二次樣條小波將暫態波形進行小波變換,提取變換后的特征信號,然后運用貝葉斯分類器來識別各種暫態。但此方法的實現過程卻太過繁瑣。文獻[29-30]考慮用最大似然法來進行擾動的分類。文獻[29]首先設計了一個濾波器把擾動分量從基頻分量中提取出來,之后用Battle-Lemarie樣條小波函數對擾動分量進行小波變換,將得到的小波系數進行特征提取后,用最大似然準則得到最終決策。該方法不但可以區分各種電壓擾動且能指出擾動的原因。文獻[30]使用基于小波的隱Markov模型的參數最優化估計方法,正確率可達到95.5%。文獻[31]進一步改進了文獻[30],提出在時域內基于規則,而在頻域內基于隱Markov模型的擾動分類方法。文獻[32]則利用擾動信號在不同尺度下的能量分布的不同,建造了一條基于多分辨率的擾動偏差曲線,根據不同擾動在此曲線上呈現出的差別,此方法不但能有效地檢測各種擾動,還能對擾動原因進行判斷。文獻[33]提出在時域而非頻域內確定擾動的起始時刻和持續時間,用一基于Vetterli-Herley-Sweldens定理的Lifting方法構成的雙正交復小波,在小波域內一個特定尺度下確定幅度,之后用二進數特征量表示不同擾動,進行分類。該文對五種暫態擾動進行分類,結果正確。
??? 但是,由于電能質量擾動涉及的特征量太多,使得分類判據復雜易錯,因此直接提取小波變換后的特征量進行擾動分類的研究并不是太多。大量的電力工作者轉為研究用人工智能的方法對擾動進行分類。
2 人工智能的應用
??? 近年來,人工智能技術發展迅速,分支眾多,除了人工神經網絡、模糊邏輯、專家系統和遺傳算法等技術,也有人研究將不同特性的智能技術結合起來進行應用,如:模糊神經網絡、小波神經網絡、模糊專家系統、自適應模糊邏輯等,以期對電力系統的運行、監試、預測、控制和規劃發揮更大的作用。
2.1 擾動的分類
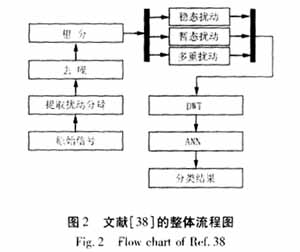
??? 早期的利用ANN對擾動進行分類的方法直接用DFT提取信號中的不同諧波次數,并且把若干次諧波次數歸為一類擾動的特征量(3次、6次和9次諧波作為一種,5次和7次諧波作為一種,11次和13次諧波作為一種)輸入不同的神經網絡[34]進行分類。由于受DFT的限制,這種方法的有效性受到限制,但這種思路卻一直延續至今。1996年,S.Santoso在文獻[35]中將雙正交小波用于檢測、定位和識別不同原因的電能質量擾動問題。作者認為可以根據在各尺度下小波系數平方值體現出的特征,用ANN等軟計算方法對電能質量的擾動進行自動識別。該文獻對將小波變換應用于電能質量的評估做了探索性的研究和有益的嘗試,但并未討論由于輸入數據的誤差所帶來的分類器判斷錯誤的問題。同年,文獻[36]采用非正交樣條小波重又對電容器投切暫態進行分析,該文作者對文獻[28]中未討論的具體實現細節進行了大量的工作。首先利用濾波器組給出了一個可用任何小波進行變換的數字設備,然后利用與文獻[35]相同的思路對暫態信號進行特征的提取。在S.Santoso思想的啟發下,F.Mo [37]提出可以利用ANN技術實現智能暫態錄波儀,以克服傳統錄波儀必須人工分析波形、閾值嚴格以及無法提供實時信息等缺點。但該文并未提供任何具體的實現步驟。B.Perunicic[38]也提出一種集數字濾波、小波變換和ANN為一體的電能質量檢測和分類的新方法。總體思路如圖2所示。該文對噪聲、次諧波畸變、周期性電壓波動、電壓凹陷、直流偏移以及振蕩等10種電能質量擾動問題進行檢測與分類,得到良好的效果。同時,該文對小波母函數的選擇、采樣率和采樣周期、監測器位置和性能等細節問題進行了全面地討論。
??? 2000年,S.Santoso利用傅氏和小波變換的方法對電能質量擾動進行了特征提取[39]后,提出了完整的基于小波的電能質量擾動波形的神經網絡分類器的實現方法[40-41]。這兩篇文章對小波理論及其在電力系統中的應用起到了重要的作用,主要流程示于圖3。其中Ident表示用傳統的方法判斷擾動是否為電 壓跌落或瞬時斷電,之所以不用小波變換處理這兩種情況是由于小波變換難以處理光滑連續的電壓跌落。 該文提出用各尺度下的小波系數作為ANN的輸入特征矢量,這使該工作的輸入量太大,于是,文獻[42-43]提出用各尺度下的能量的集合作為擾動的特征輸入矢量,不但使輸入量大為減小,而且得到很好的分類效果。文獻[44]則首先找出小波變換后含最大能量的尺度,用該尺度的小波系數與原始正弦波形的小波系數相減,并取其差值作為神經網絡的輸入變量,從而成功對8種單一擾動進行了有效區分。
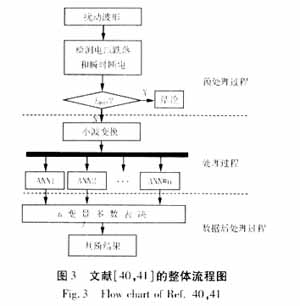
??? 但基于小波的ANN方法有時也會誤判,而且對多重擾動的分辨率低或者根本無法分辯。這是由于以下原因:1)小波變換難以檢測頻率微變擾動;2)用來作為ANN輸入量的特征量難以選取,無法精確描述各種擾動;3)送入ANN進行訓練的樣本數無法全面覆蓋各種擾動問題;4)基于小波的ANN方法訓練的結果受ANN本身結構的限制。
??? 文獻[45]對ANN進一步改進,提出使用小波模糊ANN分類器對電能質量問題進行檢測與分析,該方法首先從原始信號中提取擾動分量并去噪,然后用小波變換提取特征值,最后進行模糊ANN分析與識別,該方法大大減少了輸入ANN的特征值的個數,且對各種擾動問題有良好的適應性。文獻[46]提出ANN模糊分類器。該文首先將擾動分為三組,選取不同尺度下的小波系數分別作為這三組的ANN輸入特征量,在ANN訓練后,再通過一模糊聯想記憶變換,最大限度消除模式識別中的不確定性,從而提高系統的精確性并簡化模型。文獻[47]為電能質量的擾動的分類提供了一條全新的思路。它把模糊邏輯和專家系統結合,通過FFT/WT重新定義了8個特征量,建立相應的規則,也得到了很好的分類效果。
2.2 電能質量的提高
??? 除了用AI方法對電能質量的擾動進行分類分析外,也有文獻考慮用AI方法提高電能質量,包括用模糊方法實現電壓和無功的控制[48]、用專家系統、遺傳算法和模糊集理論實現電容器組的最優分布[49-51];用模糊邏輯分析擾動對敏感負荷的作用[52]。
3? 結論
??? 目前,在動態電能質量缺少統一的定義、統一的實踐標準和統一的對擾動進行解釋的標準的情況下,結合各種人工智能技術和先進的數學變換工具在對動態電能質量進行檢測與識別中的作用已成為一個不爭的事實。各種AI方法和數學變換均有優點也有缺陷,沒有哪一種方法是萬能的,應該結合各自的長處,對動態電能質量進行最有效的分析。目前為止,對動態電能質量進行識別使用得最多的仍然是基于小波變換的ANN技術,其它AI方法的研究尚不多見,而且,大部分的識別只針對單一擾動,而對多重擾動的分析幾乎沒有,這些問題有待進一步的研究。
 電子發燒友App
電子發燒友App





















評論