01

1.概述

隨著“雙碳”目標(biāo)的提出，新能源領(lǐng)域得到快速發(fā)展。到2060年，預(yù)測中國風(fēng)電和光伏發(fā)電裝機(jī)容量占比之和需達(dá)到約80%，發(fā)電量占比之和達(dá)到約70%[1]，電動(dòng)汽車的保有量將達(dá)到約3.9億輛[2]。SiC MOSFET和Si IGBT等功率半導(dǎo)體器件（以下統(tǒng)稱器件），作為變流器的核心部件，得到大規(guī)模的應(yīng)用。

器件的動(dòng)態(tài)特性關(guān)系到系統(tǒng)的效率、可靠性和EMC性能，受到設(shè)計(jì)人員的重點(diǎn)關(guān)注。器件動(dòng)態(tài)特性受到功率回路和柵極回路影響。功率回路特性依托于銅排結(jié)構(gòu)（大功率器件）或PCB布局（板級(jí)器件），在定型后難以調(diào)整，修改周期長。柵極回路特性依托于PCB布局和柵極元器件參數(shù)，PCB上的元器件調(diào)整方便，所以設(shè)計(jì)人員主要通過柵極參數(shù)的調(diào)整來優(yōu)化器件的動(dòng)態(tài)特性。因此，柵極參數(shù)研究是器件動(dòng)態(tài)特性研究的關(guān)鍵。

對(duì)于柵極參數(shù)的研究方法有兩種：設(shè)計(jì)和測試。

柵極參數(shù)設(shè)計(jì)是通過理論計(jì)算或建模仿真，模擬器件的開關(guān)狀態(tài)，掌握其動(dòng)態(tài)特性。常用的仿真軟件有ANSYS和MATLAB等，其核心還是理論計(jì)算。

器件動(dòng)態(tài)特性測試一般通過雙脈沖測試進(jìn)行，根據(jù)測試結(jié)果來調(diào)整柵極參數(shù)，達(dá)到最佳效果。設(shè)計(jì)人員會(huì)應(yīng)用專業(yè)的測試設(shè)備，保證測試結(jié)果的準(zhǔn)確性和可靠性。Firstack開發(fā)的ME300D測試設(shè)備因此誕生。

設(shè)計(jì)和測試相輔相成，只有設(shè)計(jì)過程，會(huì)脫離物理世界環(huán)境，使得設(shè)計(jì)結(jié)果經(jīng)不起實(shí)際工況挑戰(zhàn)；只有測試過程，會(huì)讓柵極參數(shù)優(yōu)化周期漫長，測試人員通過不停試錯(cuò)才能獲得滿意的參數(shù)。

目前市面上的的動(dòng)態(tài)測試設(shè)備通常都只停留在測試階段。Firstack通過柵極參數(shù)匹配算法，加速測試過程。Firstack 開發(fā)的智能化測試設(shè)備ME400D將具備柵極參數(shù)自動(dòng)計(jì)算匹配和自動(dòng)化測試功能，目標(biāo)提升客戶測試效率。

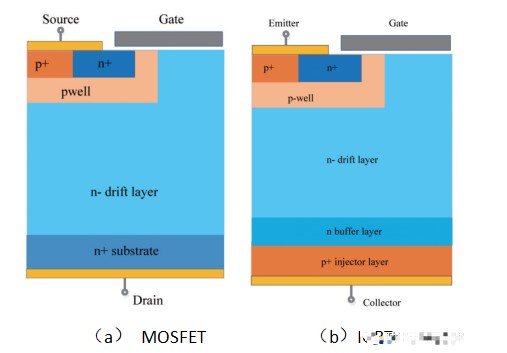
本文對(duì)器件開關(guān)過程進(jìn)行理論分析和計(jì)算，由于開關(guān)過程對(duì)稱，以關(guān)斷為例進(jìn)行計(jì)算。MOSFET和IGBT關(guān)斷過程基本類似，后續(xù)以MOSFET定義進(jìn)行命名，部分IGBT相關(guān)圖片，其C/G/E極分別對(duì)應(yīng)D/G/S極。

02

2.關(guān)斷過程研究

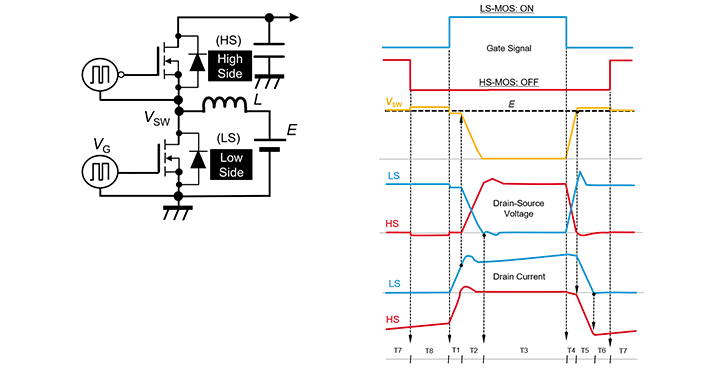
以MOSFET關(guān)斷為例，柵極電壓定義為Vgs。漏極電流定義為Id，Id的導(dǎo)通電流定義為ID，漏源電壓定義為Vds，Vds的關(guān)斷電壓定義為VDS。如圖1所示，將器件關(guān)斷過程分為3部分，0~t2為第一階段，該階段Vgs下降到米勒平臺(tái)，Id不發(fā)生變化，Vds緩慢增大，仍處于開通狀態(tài)。t2~t3為第二階段，該階段處于米勒平臺(tái)，Vgs維持米勒電壓tm，Vds上升，基本達(dá)到VDS。其形成原理在此不做贅述。t3~t4為第三階段，Vgs從米勒平臺(tái)下降到閾值電壓Vgs（th）。Id從ID下降到0。該階段Vds會(huì)產(chǎn)生電壓尖峰。

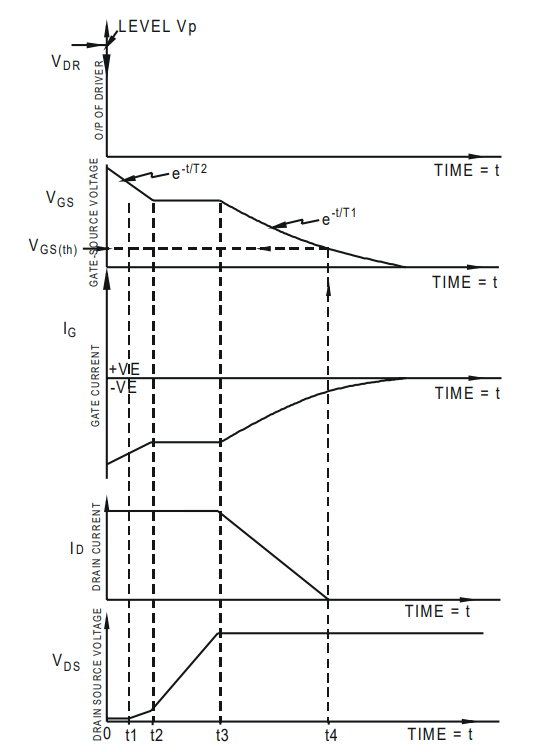
圖1 MOSFET關(guān)斷過程[3]

2.1 第一階段

t0~t2階段，驅(qū)動(dòng)從器件柵極電容抽取電荷，此時(shí)的若不考慮柵極回路雜散電感的影響，可以看作一階RC串聯(lián)放電電路，Vgs從開通電壓下降到米勒平臺(tái)的時(shí)間tf1計(jì)算公式如下， ? ? ?

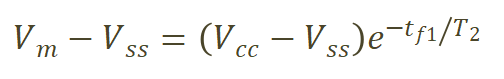
(1) ? ? ? ?

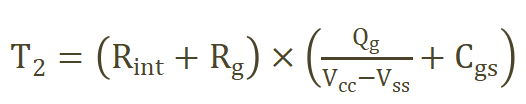
(2) ? ?

其中Vcc為驅(qū)動(dòng)的開通電壓，Vss為驅(qū)動(dòng)的關(guān)斷電壓，數(shù)值為負(fù)，Rint為器件內(nèi)部柵極電阻，Rg為外部柵極電阻，Cgs為柵極電容，Qg為器件對(duì)應(yīng)Vcc和Vss之間的柵極電荷，如圖2所示。Qg和Vds相關(guān)，通常規(guī)格書會(huì)給出典型Vds電壓下的Qm，若測試工況和典型Vds電壓相差較大，可能需要重新標(biāo)定，我司自研了滿足JEDEC標(biāo)準(zhǔn)[4]的Qg標(biāo)定方案。

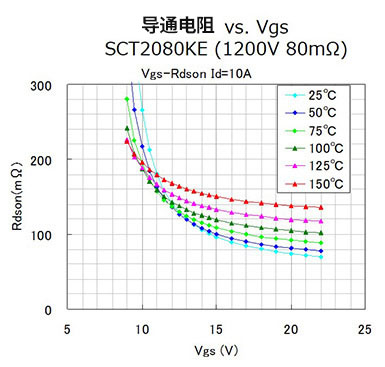
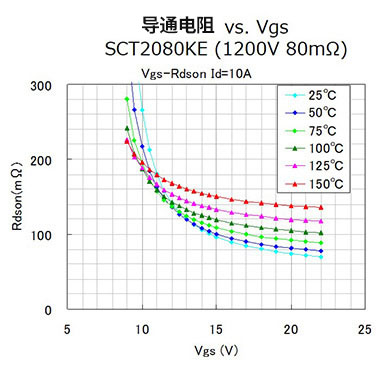
部分器件規(guī)格書會(huì)提供器件輸入電容和反向傳輸電容，也可以通過電容進(jìn)行計(jì)算，但如圖3所示，容值會(huì)隨Vds變化。特別在器件剛開始關(guān)斷，Vds較小時(shí)，變化尤其明顯，影響關(guān)斷時(shí)間評(píng)估的準(zhǔn)確性。用Qg計(jì)算等效柵極電容，會(huì)提高計(jì)算的準(zhǔn)確度。

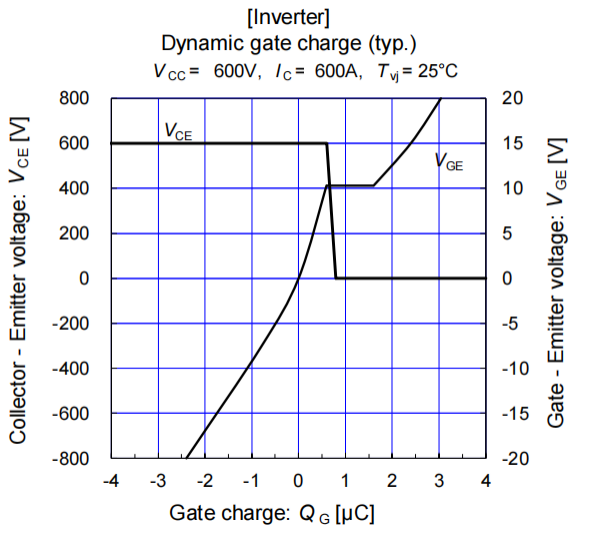
圖2 規(guī)格書Qg曲線[5]

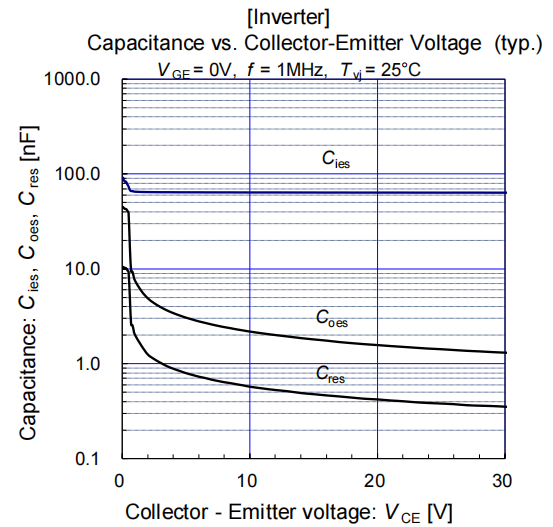
圖3 規(guī)格書電容曲線[5]

2.2 第二階段

2.2.1 米勒平臺(tái)電壓計(jì)算

米勒平臺(tái)電壓計(jì)算可分為兩部分，當(dāng)關(guān)斷電流Id較大，對(duì)應(yīng)傳輸特性曲線的Vgs電壓遠(yuǎn)超過閾值電壓Vgs(th)時(shí)，可認(rèn)為器件的傳輸特性曲線處于線性區(qū)域[6]，

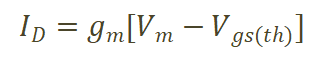
(3) gm為器件跨導(dǎo)，定義如圖4所示。

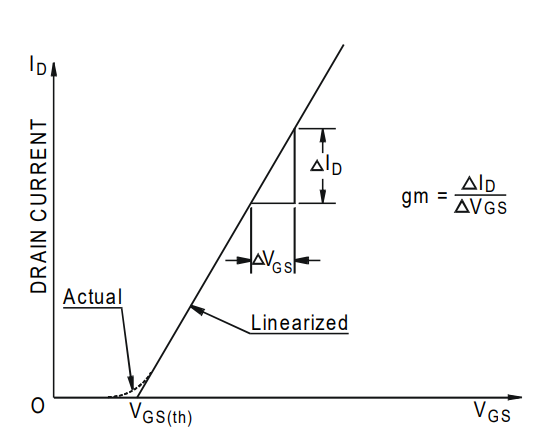
圖4 跨導(dǎo)定義

當(dāng)關(guān)斷電流較小，對(duì)應(yīng)Vgs接近閾值電壓時(shí)，

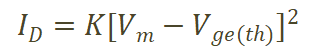
(4)

其中K是和溫度相關(guān)的常數(shù)[7]。

若器件規(guī)格書給出詳細(xì)的傳輸特性曲線，可以根據(jù)關(guān)斷電流，在圖5上取點(diǎn)來確認(rèn)米勒平臺(tái)電壓。

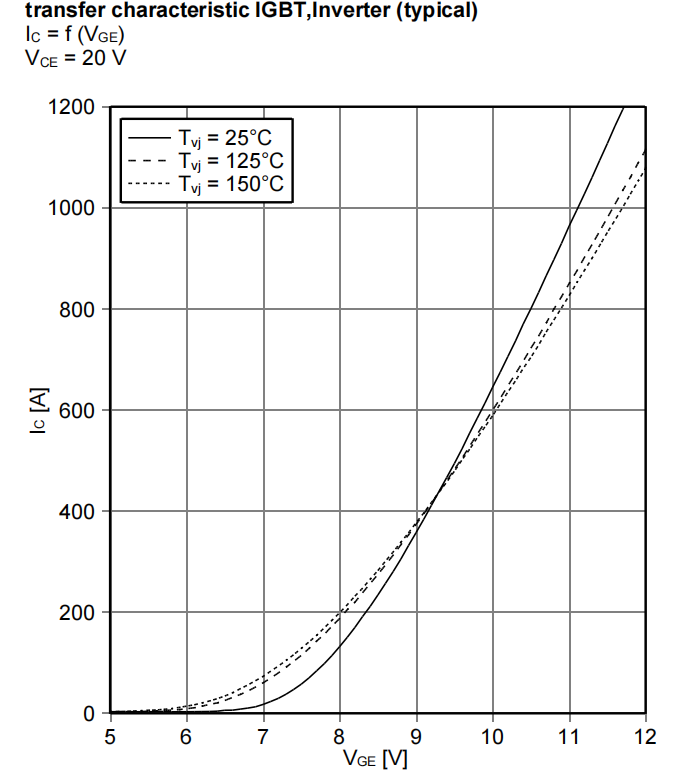
圖5 規(guī)格書傳輸特性曲線[8]

對(duì)于Si IGBT而言，米勒平臺(tái)電壓基本保持不變，如圖3所示。考慮到SiC MOSFET的短溝道效應(yīng)，其漏極電壓引起的溝道勢(shì)壘降低(DIBL)效應(yīng)明顯，米勒平臺(tái)應(yīng)為圖6所示的“米勒斜坡”[9]，根據(jù)Qg曲線可以確定米勒平臺(tái)中Vgs和Qg的變化關(guān)系。

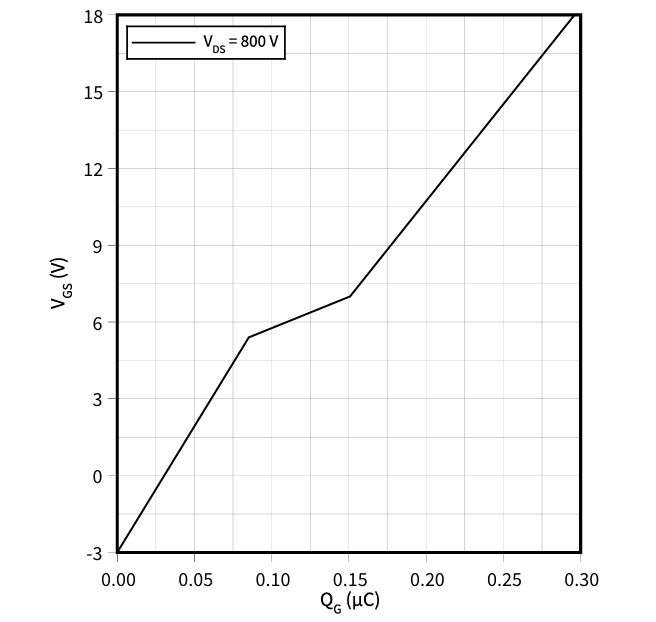
圖6?SiC MOSFET的Qg曲線

2.2.2 米勒平臺(tái)持續(xù)時(shí)間計(jì)算

當(dāng)關(guān)斷過程處于米勒平臺(tái)階段，驅(qū)動(dòng)電流全部用作給米勒電容放電，柵極電壓不變，驅(qū)動(dòng)電流不變。器件在米勒平臺(tái)時(shí)的驅(qū)動(dòng)電流Igm和米勒平臺(tái)持續(xù)時(shí)間tm計(jì)算公式如下。

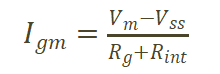
(5) 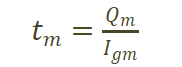(6)

其中，Qm為圖2中Vgs維持米勒平臺(tái)時(shí)的電荷量變化值。

在米勒平臺(tái)持續(xù)時(shí)間內(nèi)，Vds電壓會(huì)逐漸從器件導(dǎo)通電壓上升到關(guān)斷電壓VDS。如圖7所示，Vds往往是從米勒平臺(tái)中段才快速上升，而非米勒平臺(tái)開始時(shí)刻。Vds開始快速上升的時(shí)間tm2，在多級(jí)關(guān)斷和主動(dòng)控制型的驅(qū)動(dòng)中有重要意義。由于米勒電容（即反向傳輸電容Crss）隨Vds電壓變化，該時(shí)刻點(diǎn)難以準(zhǔn)確評(píng)估。本文給出一種近似評(píng)估方法。

以圖3所示的1200V耐壓器件為例。米勒電容在Vds小于30V時(shí)變化快。當(dāng)Vds電壓超過30V后，米勒電容基本發(fā)生變化，此時(shí)對(duì)應(yīng)的米勒電容容值Cgd=Crss(Vds=30V)，則

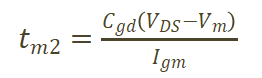
(7)

當(dāng)Vds上升到VDS，米勒平臺(tái)結(jié)束。

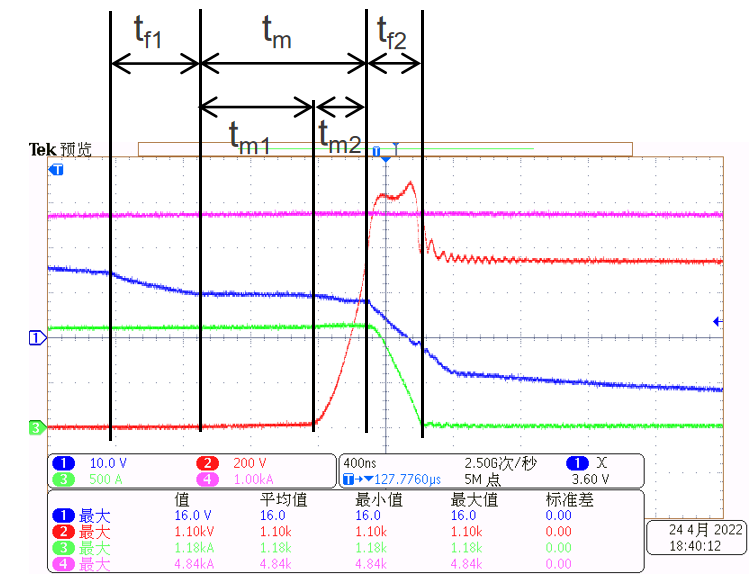
圖7?器件實(shí)際關(guān)斷過程波形(CH1:Vge,Vce, CH3:Ic)

2.3 第三階段

t3~t4為Id電流下降階段，當(dāng)Vgs下降到Vgs(th)，Id下降到0，關(guān)斷過程基本結(jié)束。其電流計(jì)算方法與第一階段類似，值得注意的是，此時(shí)Qg應(yīng)按照Vm和Vss間的柵極電荷來計(jì)算。

通過tf2和ID可以計(jì)算出第三階段電流下降階段電流變化率，用ME400D設(shè)備進(jìn)行雙脈沖測試，可計(jì)算出功率模組的功率回路雜感Lp。從而得到電壓尖峰

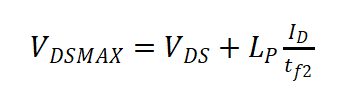
(8)

由于ID關(guān)斷過程非完全線性，且SiC MOSFET第三階段持續(xù)時(shí)間較短，容易造成偏差，通過該方法計(jì)算出的電壓尖峰會(huì)有5~10%誤差。

2.4 柵極回路電感對(duì)關(guān)斷過程的影響

由于第二階段驅(qū)動(dòng)電流基本保持不變，雜散電感對(duì)此階段沒有影響，只需要關(guān)注第一階段和第三階段。

柵極回路電感由兩部分組成，器件內(nèi)部雜散電感和驅(qū)動(dòng)PCB回路雜散電感。器件內(nèi)部雜散電感較小，和外部雜散電感相比可以忽略。因此，可以將柵極回路等效成RLC串聯(lián)電路。

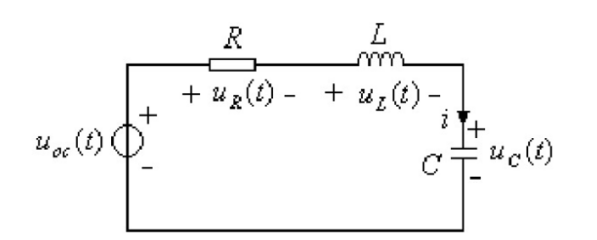
圖8?柵極回路RLC串聯(lián)等效電路

其完整的微分方程表達(dá)式為

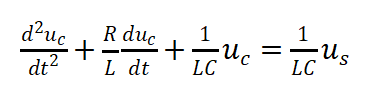
(9)

其初始狀態(tài)

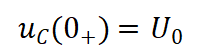
(10)

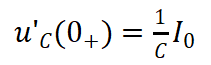
(11)

R為驅(qū)動(dòng)電阻，L為柵極回路雜感，C為器件內(nèi)外部GS電容之和，值得注意第一階段和第三階段C不相同，可以根據(jù)各自階段的Qg和Vgs求出。

以圖7電流方向?yàn)檎５谝浑A段，U0=VCC+VSS，I0=0，第三階段U0=Vm+VSS，I0=-Igm。根據(jù)微分方程列出特征方程并求出特征根

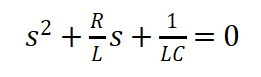
(12)

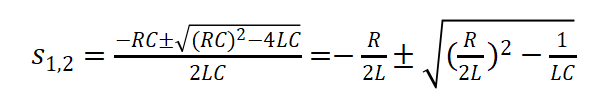
(13)

衰減常數(shù)

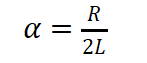(14)

諧振角頻率

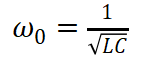(15)

當(dāng)α2 -?ω02 >0特征方程有兩個(gè)不等負(fù)實(shí)根，系統(tǒng)處于過阻尼狀態(tài)。這種狀態(tài)下，器件不會(huì)因?yàn)闁艠O形成振蕩，驅(qū)動(dòng)設(shè)計(jì)的關(guān)鍵之一，就是通過合理的驅(qū)動(dòng)參數(shù)選擇，使器件工作在該狀態(tài)。

當(dāng)α2 -?ω02 =0特征方程有兩個(gè)相等負(fù)實(shí)根，系統(tǒng)處于臨界阻尼狀態(tài)。

當(dāng)α2 -?ω02 <0特征方程有一對(duì)共軛復(fù)根，系統(tǒng)處于欠阻尼狀態(tài)。這是驅(qū)動(dòng)設(shè)計(jì)中需要避免的情況，會(huì)導(dǎo)致柵極振蕩。對(duì)于SiC MOSFET而言，柵極電荷較小，對(duì)應(yīng)C偏小，當(dāng)L過大時(shí)，容易形成欠阻尼狀態(tài)，這也是SiC MOSFET對(duì)柵極回路雜感更加敏感的原因。

通過特征根得出微分方程通解

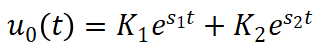
(16)

帶入初始狀態(tài)(10)(11)，可分別求出兩個(gè)階段的K1和K2。

此時(shí)就可以得出第一階段和第三階段的響應(yīng)方程，第一階段最終狀態(tài)為米勒平臺(tái)，帶入U(xiǎn)0=Vm+VSS，即可求出第一階段持續(xù)時(shí)間tf1。同理第三階段最終狀態(tài)U0=Vgs(th)+VSS，可求出第三階段持續(xù)時(shí)間tf2。

03

3.小結(jié)

(1)?本文結(jié)合驅(qū)動(dòng)電路、器件模型和測試工況三方面信息，對(duì)器件關(guān)斷過程進(jìn)行了詳細(xì)分析計(jì)算。梳理了柵極電阻、電容和電感對(duì)關(guān)斷過程的影響。

(2)?在實(shí)際應(yīng)用中，已知柵極參數(shù)，可以計(jì)算關(guān)斷各階段的時(shí)間、電壓尖峰和電壓電流變化率等；已知開關(guān)時(shí)間、電壓尖峰和電壓電流變化率等邊界條件，可以給出合理的柵極參數(shù)取值范圍。

(3)?在應(yīng)用ME400D進(jìn)行器件動(dòng)態(tài)參數(shù)測試時(shí)，輸入邊界條件，可以迅速判斷出柵極參數(shù)取值的大致范圍，并進(jìn)行自動(dòng)測試，大大提高測試效率。

*文中提及的ME400D是Firstack全新升級(jí)的SiC器件動(dòng)態(tài)特性測試設(shè)備，將于2024年發(fā)布，敬請(qǐng)期待！

[1]肖先勇,鄭子萱.“雙碳”目標(biāo)下新能源為主體的新型電力系統(tǒng)：貢獻(xiàn)、關(guān)鍵技術(shù)與挑戰(zhàn)[J].工程科學(xué)與技術(shù),2022,54(01)10.15961/j.jsuese.202100656.

[2]全球能源互聯(lián)網(wǎng)發(fā)展合作組織.中國2060年前碳中和研究報(bào)告[R]. 北京：全球能源互聯(lián)網(wǎng)發(fā)展合作組織,2021.

[3]Abhijit D. Pathak. IXYSmosfet_driver_theory_and_applications, IXYS Corporation, 2001.

[4]JEDEC JEP192. Guidelines for Gate Charge (QG) Test Method, 2022.

[5]Fuji Electric. 2MBI600XNG120-50 Datasheet, 2018.

[6]Dong Z, Wu X, Xu H, et al. Accurate analytical switching?on loss model of SiC MOSFET considering dynamic?transfer characteristic and Qgd[J]. IEEE Transactions on?Power Electronics, 2020, 35(11): 12264-12273.

[7]Wang X, Zhao Z, Li K, et al. Analytical methodology for loss calculation of SiC MOSFETs[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2018, 7(1) ; 71-83.

[8]Infineon. FF600R12ME4 Datasheet, 2013.

[9]Wang, Ning, and Jianzhong Zhang. Nonlinear capacitance?model of SiC MOSFET considering envelope of switching trajectory[J]. IEEE Transactions on Power Electronics 37. 7 (2022): 7977-7988.?

審核編輯：黃飛

?