摘? 要?
針對汽車 IGBT 模塊的主要失效原理和引線鍵合壽命短板,結合仿真分析進行了功率循環試驗設計,結溫差?ΔTj 和流經鍵合線的電流 IC 是影響鍵合點壽命的主要加速因子,中間溫度(Tjm)是影響鍵合點壽命的重要因子。傳統功率循環壽命試驗需采用大量的試驗樣本,文章采用單根鍵合引線作為試驗獨立樣本,極大程度地減少了試驗所需的樣本數,同時通過壓降參數 VCE(sat)?的微小變化相對準確地獲取到 IGBT 模塊內部鍵合線的脫落趨勢,結合壽命模型和威布爾統計方法,對鍵合點壽命進行統計分析,最終獲得功率循環壽命曲線。利用新的功率循環壽命統計方法可將試驗成本和試驗周期減少 80%。
0? 引言
隨著電動汽車的高速發展,作為其核心部件的IGBT 模塊的可靠性也倍受關注。IGBT 的壽命研究國內外已有不少研究成果,但是對于汽車用的 IGBT 模塊的研究較少。汽車 IGBT 模塊應用工況相對其他應用工況更加惡劣,在汽車運行過程中,啟停和加減速頻繁,對應的是 IGBT 模塊的功率變化,IGBT 結溫也會隨之不斷循環變化,溫度變化產生的熱應力會使模塊內部層次間產生蠕變熱疲勞,直至 IGBT 失效。針對汽車IGBT 特殊的應用工況條件,準確地評價 IGBT 模塊的熱循環壽命需求非常迫切。
功率循環試驗是 IGBT 模塊常用的加速壽命試驗方法之一,通過給 IGBT 模塊通斷直流電流并結合外部冷卻水冷卻,使芯片結溫在可控的溫度范圍內變化,該方法是通過加速方法模擬 IGBT 模塊在應用工況中的溫度變化,定量評價熱疲勞的損傷,是應用壽命預測重要的評價手段。
1? 功率循環壽命退化原理
服役狀態下的 IGBT 模塊處于亞穩定狀態,其材料和結構會隨著時間的推移發生狀態改變或退化。IGBT 模塊在整個壽命周期內,會經歷數萬至數百萬次的溫度循環沖擊,這期間熱應力的反復作用會使材料發生疲勞,造成模塊封裝結構的逐漸退化。IGBT 模塊封裝結構的退化主要表現在模塊的電學和熱學性能的退化上。
1.1? 熱退化
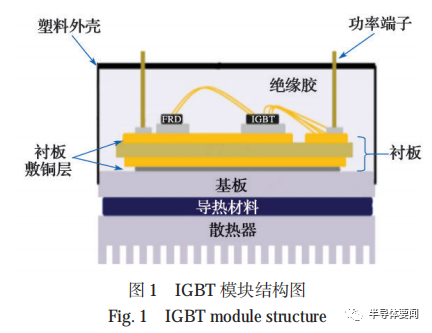
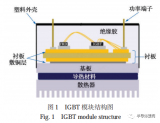
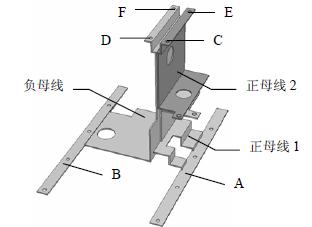
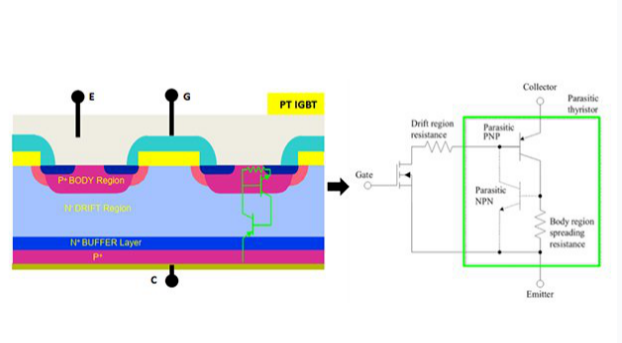
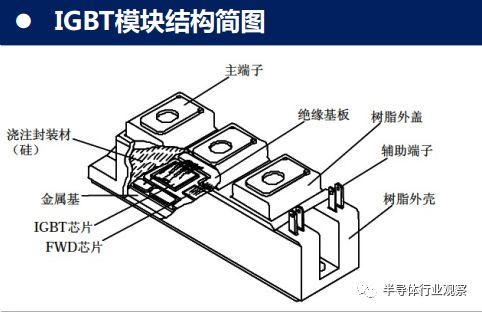
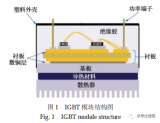
IGBT 模塊(結構圖見圖 1)在應用中的電壓、電流不是恒定的,而是隨著汽車運行速度和載荷的變化而變化,從而使模塊溫度不斷變化。由于模塊芯片、芯片焊層、DBC 等層次的熱膨脹系數不完全一致,當模塊受到芯片溫度的循環沖擊時,不同材料會產生不同程度的受熱膨脹和冷卻收縮,從而使模塊的各層材料之間產生交變的應力,造成結構的松弛和材料裂紋的萌生,使得導熱系數等熱參數退化。當 IGBT 模塊的焊料出現裂紋和分層時,從芯片到模塊底部散熱器之間的有效傳熱面積就會減小,造成模塊熱阻 Rth 的增大。IGBT 模塊熱阻的增大又會降低模塊的傳熱性能,導致芯片結溫 Tj 升高。
1.2? 電參數退化
在應用工況中,IGBT 模塊材料的損傷會影響其外部電學特性,使模塊的電氣參數發生變化,這些電氣參數包括壓降 VCE(sat)?和 VF、柵極閾值電壓 VGE(th)、柵極電流 IGES 等。鍵合線與芯片之間熱膨脹系數不匹配引起的熱應力會造成鍵合線脫落,導致鍵合線接觸電阻增大,進而使得 IGBT 模塊的導通電阻 Ron 增大,飽和壓降 VCE (sat)?升高。此外,為了連接 IGBT 芯片元胞和發射極,進行芯片與襯板的引線鍵合,芯片表面會覆蓋一層鍍層金屬。當鍍層金屬受到溫度沖擊時,晶粒會產生塑性變形 ,引起金屬化重構。鍍層金屬的演化會減小其有效橫截面積,增大整個鍍層金屬的電阻,影響模塊的飽和壓降 VCE(sat)。
2? 鍵合熱機仿真
IGBT 模塊工作過程中涉及到電流場、溫度場、應力場等多個物理場相互作用的影響,電流場產生功率損耗,功率損耗引起的焦耳熱是溫度場中的熱源,模塊溫度的波動及溫度場的不均勻分布會使模塊各層之間產生熱應力,進而模塊發生形變。模塊形狀的改變又會引起溫度場的變化和電流分布的改變,因此,在進行 IGBT 模塊鍵合線應力仿真時,應考慮多個物理場之間相互耦合的情況。本文建立的 IGBT 模塊實體模型如圖 2 所示。在芯片表面有源區施加發熱載荷,模擬芯片發熱時的溫度場分布,計算鍵合線的累積塑性變形損傷及其具體發生的位置。
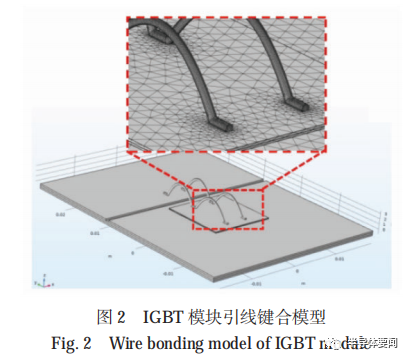
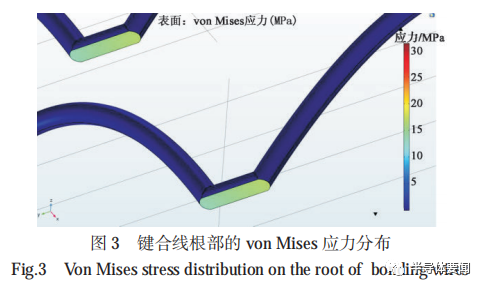
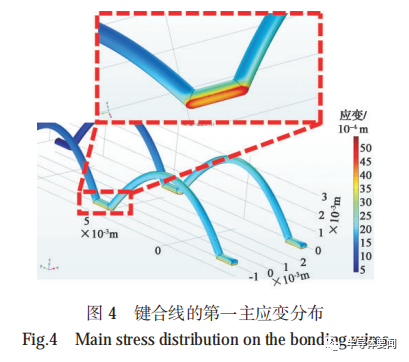
圖 3 給出了鍵合線根部的 von Mises 應力分布。可以發現,在鍵合點處產生 von Mises 應力的最大值,鍵合線根部出現應力集中現象。提取鍵合線上的第一主應變分布,如圖 4 所示,發現在應力較大的鍵合線根部位置鍵合線的第一主應變最大。功率循環試驗中IGBT 模塊鍵合線的失效,往往是在鍵合點處產生裂紋,裂紋擴展導致鍵合線脫落。
3? 試驗設計
3.1? 功率循環試驗方法
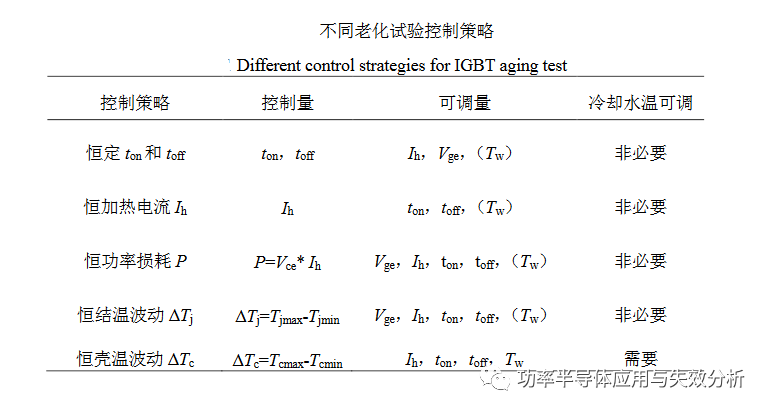
大功率 IGBT 模塊功率循環常用的試驗方法有恒定結溫升?ΔTj 、恒定功率 P 和恒定電流 IC。恒定結溫升ΔTj 和恒定功率 P 主要是針對焊層的退化,其中恒定結溫升?ΔTj 的試驗模式更加普遍;恒定電流 IC 試驗模式則主要用于評價鍵合點的壽命。
3.1.1 恒定結溫升 ΔTj 模式
恒定結溫升 ΔTj 試驗模式即在試驗過程中,Ton 和Toff 保持不變,實時調整 IC 的值,使?ΔTj 恒定。該試驗模式下,隨著產品熱特性的退化,維持結溫升?ΔTj 穩定需要不斷地減小電流 IC。恒定結溫升 ΔTj 的試驗模式在軌道交通用高壓 IGBT 模塊的芯片焊層熱疲勞評價中被廣泛應用。對于軌道交通用 IGBT 模塊通常會對引線鍵合點進行涂膠保護,引線不會輕易脫落,其壽命短板為芯片焊層的分層和收縮。結溫變化值是焊層熱疲勞退化的主要因子,受電流大小影響較小,故軌道交通用高壓IGBT 模塊試驗采用恒定結溫升?ΔTj 的模式比較合適。
3.1.2? 恒定電流 IC 試驗模式
恒定電流 IC 試驗模式即為在試驗過程中,Ton, Toff,IC 全部保持不變。在試驗開始的時候通過前期調整使Ton, Toff, IC 滿足設定的?ΔTj 的要求,在試驗過程中不再對這些參數進行調節。這種試驗模式下,隨著產品熱退化和電退化綜合效應導致?ΔTj 越來越大。對于汽車用IGBT 模塊,由于封裝工藝和材料等與高壓模塊存在差異且考慮成本因素,對模塊的引線鍵合點通常未涂覆保護膠,鍵合點是 IGBT 模塊壽命的短板,電參數退化是主要的退化原理,通常采用恒定電流 IC 模式進行試驗。AQG324 汽車模塊標準也做了同樣的規定說明。
3.1.3? 熱敏系數測試
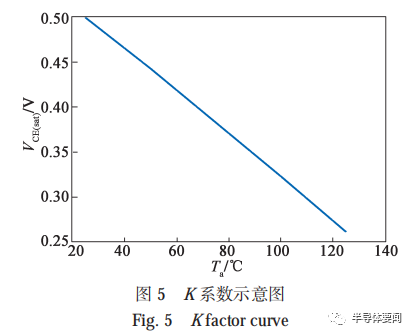
在進行功率循環前,試驗人員需要對 IGBT 模塊進行熱敏系數(也稱 K 系數)的測量。在小電流下,結溫和電壓 VCE 呈線性關系。所以,在不同溫度下對壓降VCE 進行精準的標定,獲取小電流下壓降與溫度的關系曲線,該曲線的斜率即為 IGBT 的 K 系數,K 系數示意圖見圖 5。試驗過程中只需獲取小電流下模塊的壓降即可反推出芯片的結溫。
3.2? 威布爾統計方法介紹
威布爾分布在可靠性工程領域具有舉足輕重的地位,該分布模型是功率半導體器件常用的壽命分布模型。本文研究的 IGBT 鍵合點失效主要由于材料壽命引起,其壽命分布可以用兩參數威布爾統計分布來描述?,其累積失效率計算公式為式中:
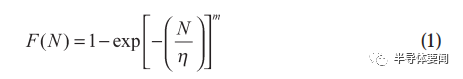
m 為形狀參數;η?為真尺度參數;N 為器件失效周期數。
將統計的鍵合點壽命數據進行整理,通過作圖法,可以獲得形狀參數m和真尺度參數η的值,利用上述值,便可輕松算得樣品的壽命?為

式中:R 為規定的可靠度。
3.3???試驗方案設計
3.3.1 壽命模型
功率半導體壽命常用模型為
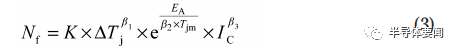
式中:Nf 為模塊壽命;K 為玻爾茲曼常數;Tjm 為平均結溫;EA 為激活能;β1, β2, β3 為計算值,與功率器件結構及材料有關,無實際物理意義。
對于功率IGBT模塊,式中的激活能EA通常取0.168eV ?。上述模型中加速因子主要為?ΔTj, Tjm, IC。本文以此模型為基礎進行試驗方案的設計。
3.3.2 試驗設計
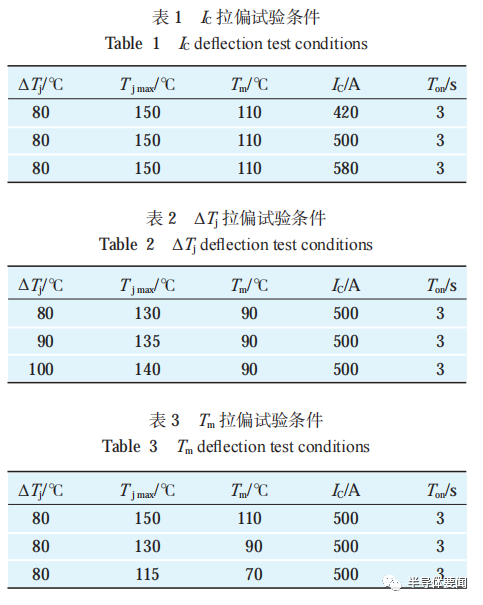
試驗采用恒定電流 IC 的模式。對 ΔTj, Tjm, IC3 個加速因子進行拉偏試驗,當對一個參數進行拉偏時,其他 2 個參數保持一致。拉偏方案具體見表 1~?表 3。為滿足設定的條件,可以適當調整 IGBT 柵極電壓 VGE 和關斷時間 Toff。
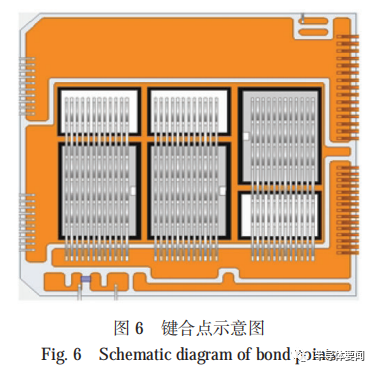
對于壽命分布的統計,通常都是取模塊壓降 VCE(sat)退化 5% 的循環次數作為模塊的截止壽命 ,這種方式是將 IGBT 模塊整體作為黑匣子處理,忽略了其失效的過程細節。在做壽命分布的時候需要大量的樣本才能獲取比較準確的壽命值,通常需要單個試驗拉偏條件大于 10?只的樣本數量,這無疑需要巨大的經濟成本和時間成本。針對汽車IGBT模塊鍵合點脫落的失效模式,本文研究采用以鍵合點作為樣本子樣,進行功率循環壽命統計。圖 6 所示模塊是一種汽車用半橋 IGBT 模塊,其一個橋臂有 144 個鍵合點,即每只模塊可視為144 個樣本子樣,因此可以通過較少的幾只模塊的試驗數據,得到大量鍵合點的壽命,這將大大減少試驗的經濟成本和時間成本,同時能夠更準確獲取鍵合點壽命的循環次數。
4? 試驗結果
4.1? 試驗數據統計
本文的試驗設計采用恒定電流 IC 的試驗模式。功率循環試驗的熱疲勞效應導致鍵合點與芯片金屬層界面裂紋生長,每次鍵合點的脫落,IGBT 模塊的壓降VCE(on)?會明顯增大,形成一個明顯的臺階,可以方便試驗人員對鍵合點脫落時對應的循環周次數進行統計,如圖 7 所示。
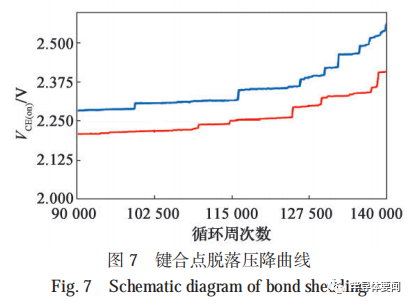
在鍵合點脫落數量較少的情況下,每個鍵合點的脫落會產生一個相對固定的 ΔVCE(on)。當鍵合點脫落數量達到一定數量后,每個鍵合點脫落會導致壓降的增加值與初始的 ΔVCE(on)?不再呈線性關系,影響到循環周次數對應的鍵合點脫落數量統計,可以采用定數截尾的方式進行試驗來減小統計誤差。每個壓降突變處鍵合點的脫落數量可以近似計算為

式中:V2 為臺階上沿值;V1 為臺階下沿值;ΔVCE(on)?為單根鍵合點脫落所增加的壓降值。
隨著產品性能的退化,芯片的溫度也會大幅增加,IGBT?芯片通常為正溫度系數,可對式?(4)?進行系數修正,每個壓降突變處鍵合點的脫落數量可近似計算為

根據試驗過程曲線,按照式 (4) 或式 (5) 的計算方法,統計不同循環周次數對應的鍵合點脫落數量,如圖 8 所示(圖中點的個數即為鍵合點脫落數量)。

4.2? 數據分析及壽命計算
按照威布爾分布計算方法對鍵合點脫落統計數據進行分析,獲取在某一累計失效率下的 IGBT 模塊功率循環壽命,如圖 9 所示。威布爾參數計算方法已經非常成熟,本文不再贅述。
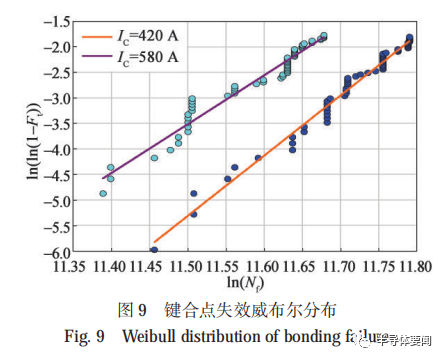
本文以鍵合點累積失效率為 10% 作為模塊的壽命(也稱為 B10?壽命),計算得到不同試驗條件下的IGBT 模塊功率循環壽命,如表 4~?表 6 所示。
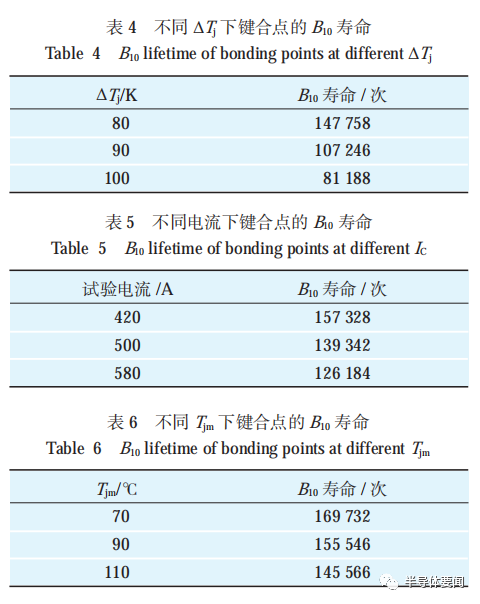
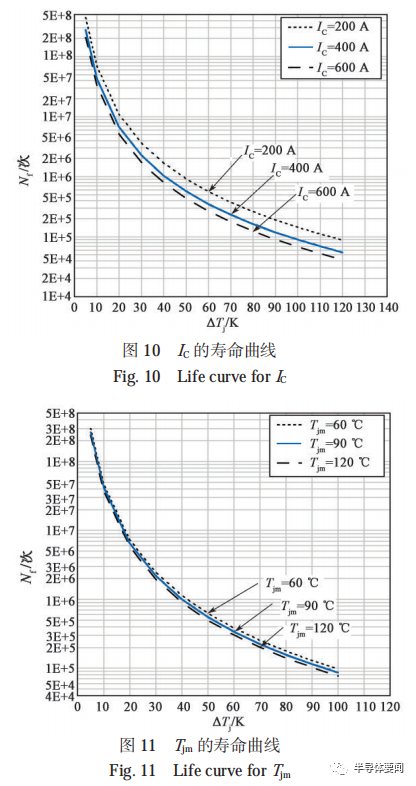
基于壽命模型式?(3)?對上述試驗數據代入進行計算,獲取系數?β1, β2, β3 值,通過計算的壽命模型可擬合得到在不同加速因子下的二維功率循環壽命曲線如圖 10?和圖 11 所示。圖 10?和圖 11 的曲線表明,IC 對鍵合點壽命的影響較大,是影響鍵合點壽命的主要加速因子;Tjm 對鍵合點壽命的影響相對較小,但也是影響鍵合點壽命的重要加速因子。失效模塊解剖圖如圖所示 12。

對完成試驗的模塊進行解剖分析,模塊鍵合點有明顯剝離脫落,失效位置為鍵合點根部,佐證了前文的鍵合熱機仿真的失效模式。
5???結語
本文基于汽車 IGBT 模塊功率循環壽命的研究,從失效原理、試驗方法、壽命模型和統計模型等多個角度進行闡述,針對汽車 IGBT 模塊的鍵合點壽命短板,進行了功率循環試驗設計。本文提出基于鍵合點作為樣本子樣的壽命統計方法,相比傳統以 IGBT 模塊作為樣本的壽命統計方法,該方法可以大幅度減少試驗樣本數量 , 節省巨大的時間成本和經濟成本 , 并提升壽命評價的準確性,具有很好的工程應用價值。
編輯:黃飛
 電子發燒友App
電子發燒友App







































評論