John Ardizzoni 和 Jonathan Pearson
引言
大多數現代高性能ADC使用差分輸入抑制共模噪聲和干擾。 由于采用了平衡的信號處理方式,這種方法能將動態范圍提高2倍,進而改善系統總體性能。 雖然差分 輸入型 ADC也能接受單端輸入信號,但只有在輸入差分信號時才能獲得最佳ADC性能。 ADC驅動器專門設計用于提供這種差分信號的電路—可以完成許多重要的功能,包括 幅度調整、單端到差分轉換、緩沖、共模偏置調整和濾波等。 自從推出 AD8138,1 以后,差分ADC驅動器已經成為數據采集系統中不可或缺的信號調理元件。
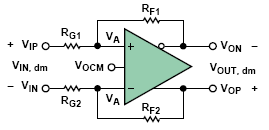
圖1:差分放大器
圖1是一種基本的完全差分電壓反饋型ADC驅動器。 這個圖與傳統運放的反饋電路有兩點區別:差分ADC驅動器有一個額外的輸出端(V上)和一個額外的輸入端(VOCM) 。 當驅動器 與差 分 輸入型ADC連接時,這些輸入輸出端可以提供很大的靈活性。
與單 端 輸出相反,差 分ADC驅動器產生平衡的差分輸出信號—相對于VOCM—在V上與V上 之間。 這里的P指的是正,N指的是負。 VOCM輸入信號控制輸出共模電壓。 只要輸入與輸出信號處于規定范圍內,輸 出共模電壓必定等于VOCM輸入端的電壓。 負反饋和高開環增益致使放大器輸入端的電壓VA+和V一個- 實質上相等。
為了便于后面的討論,需要明確一些定義。 如果輸入信號是平衡信號,那么V知識產權和V在 相對于某個公共參考電壓的幅度應該是相等的,相位則相反。 當輸入信號是單端信號時,一個輸入端是固定電壓,另一 個輸入端的電壓相對這個輸入端變化。 無論是哪種情況,輸入信號都被定義為 在知識產權 –在在。
差模輸入電壓V在, dm和共模輸入電壓V在, cm的定義見公式1和公式2。
?
| ? |
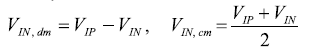
| ? | ??? | (1, 2) |
?
雖然這個共模電壓的定義應用于平衡輸入時很直觀,但對單端輸入同樣有效。
輸出也有差模和共模兩種,其定義見公式3和公式4。
?
| ? |
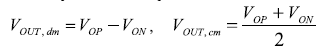
| ? | ??? | (3, 4) |
?
需要注意實際的輸出共模電壓V外, cm和VOCM輸入端之間的差異,這個差異決定了輸出共模電平。
對差分ADC驅動器的分析比對傳統運放的分析要復雜得多。 為了簡化代數表達式,暫且定義兩個反饋系數β1和β2,見公式5和公式6。
?
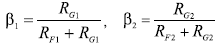 |
??? | (5, 6) |
?
在大多數ADC驅動應用中 β1= b2, 但含有 V知識產權在在在OCM, 1和2項的 在外, dm通用閉環公式對于了解β失配對性能的影響非常有用。在外, dm 的計算見公式7,其中包括了與頻率相關的放大器有限開環電壓增益A(s)。
?
| ? |
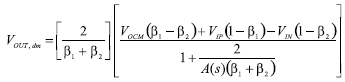
| ? | ??? | (7) |
?
當 b1≠ b2, 差分輸出電壓取決于VOCM—這不是理想的結果,因為 它產生了偏移,并且在差分輸出中有過大的噪聲。 電壓反饋架構的增益帶寬積是常數。 有趣的是,增益帶寬積中的增益是兩個反饋系數平均值的倒數。
當 b1= b2 ≡ |?β, 公式7可以被簡化為公式8。
?
| ? |
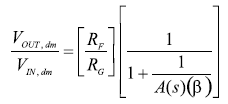
| ? | ??? | (8) |
?
這個表達式大家可能更加熟悉。 當 A(s) → ∞. 理想的閉環增益可以簡化為RF/RG 增益帶寬乘積公式看起來也很熟悉,其中的"噪聲增 益 "與傳統運放一樣,等于1/β。
反饋系數匹配的差分ADC驅動器的理想閉環增益見公式9。
?
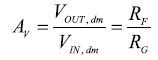 |
??? | (9) |
?
輸出平衡是差分ADC驅動器的一個重要性能指標,它分兩個方面:幅度平衡和相位平衡。 幅度平衡用于衡量兩個輸出在幅度方面的接近 程度,對于理想放大器來說它們是完全一致的。 輸出相位平衡用于衡量兩個輸出的相位差與180°的接近程度。 輸出幅度或相位的任何 失衡都會在輸出信號中產生有害的共模分量。 輸出平衡誤差(公式10)是差分輸入信號產生的輸出共模電壓與相同輸入信號產生的輸 出差模電壓的對數比值,單位是dB。
?
| ? |
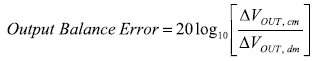
| ? | ??? | (10) |
?
內部共模反饋環路迫使V哎呀??, cm等于輸入端VOCM的電壓,從而達到完美的輸出平衡。
將輸入端接到ADC驅動器
處理高速信號的系統經常會用到ADC驅動器。 分隔距離超 過信號波長一小段的器件之間必須用具有受控阻抗的電氣傳輸線連接,以避免 破壞信號完整性。 當傳輸線的兩端用其特征阻抗端接時可以取得最佳性能。 驅動器一般放在靠近ADC的地方,因此在它們之間不要求使 用受控阻抗連接。 但到ADC驅動器輸入端的引入信號連接通常很長,必須采用正確電阻端接的受控阻抗連接。
不管是差分還是單端,ADC驅動器的輸入阻抗必須大于或等于理想的終端電阻值,以便添加的終端電阻RT能與放大器輸入端并聯達到 要求的電阻值。 本文討論的例子中的所有ADC驅動器都設計成具有平衡的反饋比,如圖2所示。

圖2:差分放大器的輸入阻抗
因為兩個放大器輸入端之間的電壓被負反饋驅動到零,因此兩個輸入端處于連接狀態,差分輸入阻抗R在就簡單地等于2×RG。 為了匹配傳輸線阻抗 RL,需要將由公式11計算得到的電阻RT跨接在差分輸入端。 圖3給出了典型的電阻值,其中 RF= RG = 200 Ω, 理想的 RL, dm= 100 Ω,RT= 133 Ω.
?
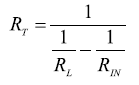 |
??? | (11) |
?
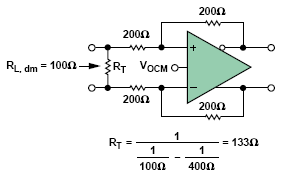
圖3:匹 配100Ω傳輸線。
單端輸入的端接更加麻煩。 圖4描述了采用單端輸入和差分輸出的ADC驅動器工作原理。
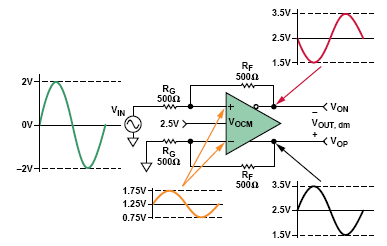
圖4:采用單端輸入的ADC驅動器例子。
雖然輸入是單端的,但 VIN, dm 等于 V在. 因為電阻RF和RG 是相等和平衡的,因此增益是1,而且差分輸出 在上–在上, 等于輸入,即 4 V p-p. 在出,厘米= VOCM = 2.5 V ,而且從下方的反饋電路可以看出,輸入電壓 VA+ 和 V一個– 等于 V上/2.
根據公式3和公式4, V上= VOCM+ V在/2, 即2.5V±1V的同相擺幅; V上= VOCM–在在/2, 即2.5V±1V的反相擺幅。 這樣,VA+ 和 V一個– 的擺幅等于 1.25V±0.5V。 The 必須由 V在 提供的電流交流分量等于 (2 V – 0.5 V)/500 Ω = 3 mA, 因此到地的電阻必須匹配,從 V在, 看過去為 667 Ω.
當每個環路的反饋系數都匹配時,公式12 就是計算這個單端輸入電阻的通式,其中R在, se是單端輸入電阻。
?
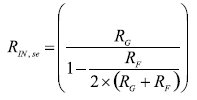 |
??? | (12) |
?
這是計算終結電阻的出發點。 然而值得注意的是,放大器增益公式基于零阻抗輸入源的假設。 由于存在單端輸入造成的不平衡而必須 加以匹配的重要源阻抗只會增加上面RG的阻值。 為了保持平衡,必須增加下面RG的阻值來實現匹配,但這會影響增益值。
雖然可以為解決端接單端信號問題而采用一個封閉形式的解決方案,但一般使用迭代的方法。 在下面的例子中這種需求將變得很明顯。
在圖5中,為了保持低的噪聲,要求單端到差分增益為1,輸入終結電阻為50Ω,反饋和增益電阻值在200Ω 左右。
根據公式12可以算出單端輸入電阻為267Ω。公式13表明,并聯電阻RT應等于61.5Ω,才能將267Ω輸入電阻減小至50 Ω.
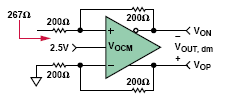
圖5:單端輸入阻抗
?
| ? |
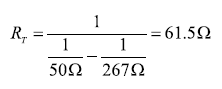
| ? | ??? | (13) |
?
圖6是帶源電阻和終端電阻的電路。 帶50Ω源電阻的源開路電壓為2Vp-p。 當源用50Ω端接時,輸入電壓減小到1V p-p,這個電壓也是單位增益驅動器的差分輸出電壓。
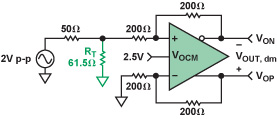
圖6:帶源電阻和終端電阻的單端電路。
這個電路初看起來非常完整,但不匹配的61.5Ω電阻與50Ω的并聯并增加到了上面的RG電阻,這就改變了增益和單端輸入電阻,并且造成 反饋系數失配。 在低增益情況下,輸入電阻的變化很小,暫時可以忽略,但反饋系數仍然必須匹配。 解決這個問題的最簡單方法是增加下面 RG的阻值。 圖7是一種Thévenin等效電路,其中上方的并聯組合用作源電阻
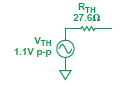
圖7:輸入源的Thévenin等效電路
有了這種替代方案后,就可以將2 7. 6Ω的電阻RTS 增加到下面的環路中實現環路反饋系數的匹配,如圖8所示。
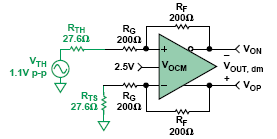
圖8:平衡的單端端接電路
注意,1.1V p -p的Thévenin電壓要大于1V p-p的正確端接電壓,而每個增益電阻增加了2 7. 6Ω,降低了閉環增益。 對于大電阻(>1kΩ) 和低 增 益(1或2)來說這些相反的效應基本抵消,但對于小電阻或較高增益來說并不能完全抵消。
圖8所示電路現在分析起來就很容易了,其中的差分輸出電壓可以用公式14計算。
?
| ? |
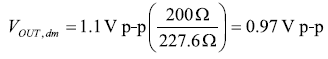
| ? | ??? | (14) |
?
差分輸出電壓并不完全等于理想的1Vp-p,但可以通過修改反饋電阻實現最終獨立的增益調整,如公式15所示.
?
| ? |
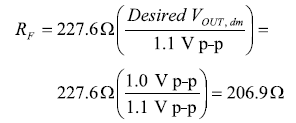
| ? | ??? | (15) |
?
圖9是用標準1%精度電阻實現的完整電路。
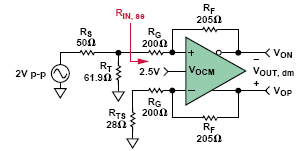
圖9:完整的單端端接電路。
觀察: 參考圖9,驅動器的單端輸入電阻RJ 米, s e由于RF和RG的改變而變化。 驅動器上端環路的增益電阻是200Ω ,下端環路的電阻是 200 Ω + 28 Ω = 228 Ω 。 在不同增益電阻值的情況下計算RJ 米, s e首先要求計算兩個β值,見公式16和公式17。
?
| ? |
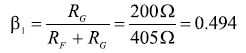
| ? | ??? | (16) |
| ? |
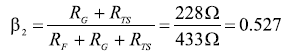
| ? | ??? | (17) |
?
輸入電阻 R在, se的計算見公式18。
?
| ? |
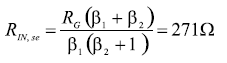
| ? | ??? | (18) |
?
這個值與原來計算的267Ω稍有不同,但對RT的計算沒有顯著的影響,因為R 在如果T 是并聯的關系。
如果需要更精確的總體增益,可以使用更高精度或串聯的可調電阻。
述的單次迭代方法非常適合閉環增益為1或2的場合。 增益越高,RTS的值越接近RG值,用公式18計算的R在, se 值與用公式12計算的R在, se值之間的差異就越大。 在這些情況下要求采用多次迭代。
多次迭代并不難實現:最近ADI公司發布的可下載的差分放大器計算工具, ADIsimDiffAmp? (參考文獻2)和 ADI Diff Amp Calculator?(參 考文獻3)足以擔當此任,它們能在幾秒內完成上述計算。
輸入共模電壓范圍
輸入共模電壓范圍(ICMVR)規定了正常工作狀態下可以施加于差分放大器輸入端的電壓范圍。 在這些輸入端上呈現的電壓可以被稱為ICMV、 V碳化或VA。 這個ICMVR指標經常被誤解。 最常遇到的難題是確 定差分放大器輸入端的實際電壓,特別是相對于輸入電壓而言。 知道變量V±在厘米 β和VOCM的值后,當β不相等時使用通式19、當β相等時使用簡化公式20就可以計算出放大器的輸入電壓(VA)。±
?
| ? |
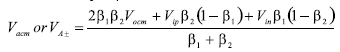
| ? | ??? | (19) |
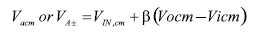 |
??? | (20) |
?
記住V一個始終是按比例縮小的輸入信號,這一點非常有用(見圖4)。 不同的放大器類型有不同的輸入共模電壓范圍。 ADI公司的高速差分ADC驅動器有兩種輸入級配置,即中心型和偏移型。 中心型ADC驅動器的輸入電壓離每個電壓軌有約1V的距離(因此叫中心型)。 而偏移 型輸入級增加了兩個晶體管,允許輸入端電壓擺幅更接近–VS軌。 圖10是一個典型差分放大器(Q2和Q3)的簡化輸入原理圖。
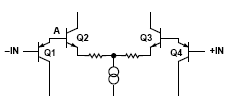
圖10:具有偏移型ICMVR的簡化差分放大器。
偏移型輸入架構允許差分放大器處理雙極性輸入信號,即使放大器是采用單電源供電,因此這種架構非常適合輸入是地或地電平以下的單電源應用。 在輸入端增加的 PNP晶體管(Q1和Q4)可以將差分對的輸入電壓向上偏移一個晶體管的V是電壓 。 例如,當-IN端電壓為-0.3V時,A點電壓將為0.7V,允許差分對正常工作。 沒有 PNP(中心型輸入級)時,A點的-0.3V電壓將使NPN差分對處于反向偏置狀態,因而無法正常工作。
表1提供了ADI公司ADC驅動器的多數指標一覽表。 對這張表粗略一看就能發現哪些驅動器具有偏移型ICMVR,哪些沒有。
表1:高速ADC驅動器的指標。
?
| ADC驅動器 | ICMVR | 在OCM | 過采樣模擬前端增益為10時的ADC噪聲預算 | ||||||||||
| 供電電壓 | 供電電壓 |
輸出擺幅(V) ? |
我供應(毫安) | ||||||||||
| 產品型號 | 帶寬(MHz) | 壓擺率(V/μs) | 噪聲(nV) |
±5 V ? |
±5 V |
±3.3 V ? |
±3 V ? |
±5 V |
±5 V ? |
±3.3 V ? |
±3 V ? |
||
| AD8132 | 360 | 1000 | 8 |
–4.7 至 +3 ? |
0.3 到 3 | 0.3 到 1.3 | 0.3 到 1 |
±3.6 ? |
1 到 3.7 |
— ? |
0.3 到 1 |
±1 ? |
12 |
| AD8137 | 76 | 450 | 8.25 | –4 至 +4 | 1 到 4 | 1 到 2.3 | 1 到 2 | ±4 | 1 到 4 | 1 到 2.3 | 1 到 2 | RR | 3.2 |
| AD8138 | 320 | 1150 | 5 | –4.7 至 +3.4 | 0.3 到 3.2 | — |
— ? |
±3.8 | 1 到 3.8 |
— ? |
— ? |
±1.4 | 20 |
| AD8139 | 410 | 800 | 2.25 | –4 至 +4 | 1 到 4 |
— ? |
— ? |
±3.5 | 1.5 到 3.5 |
— ? |
— | RR | 24.5 |
|
ADA4927-1/ ADA4927-2 |
2300 | 5000 | 1.4 | –3.5 至 +3.5 | 1.3 到 3.7 |
— ? |
— ? |
±3.5 | 1.5 到 3.5 |
— ? |
— ? |
±1.2 | 20 |
|
ADA4932-1/ ADA4932-2 |
1000 | 2800 | 3.6 | –4.8 至 +3.2 | 0.2 到 3.2 |
— ? |
— ? |
±3.8 | 1.2 到 3.2 |
— ? |
— ? |
±1 | 9 |
|
ADA4937-1/ ADA4937-2 |
1900 | 6000 | 2.2 |
— ? |
0.3 到 3 | 0.3 到 1.2 |
— ? |
— ? |
1.2 到 3.8 | 1.2 到 2.1 |
— ? |
±0.8 | 39.5 |
|
ADA4938-1/ ADA4938-2 |
1000 | 4700 |
2.6 ? |
–4.7 至 +3.4 | 0.3 到 3.4 |
— ? |
— ? |
±3.7 |
1.3 到 3.7 ? |
— ? |
— | ±1.2 | 37 |
|
ADA4939-1/ ADA4939-2 |
1400 | 6800 |
2.6 ? |
— ? |
1.1 到 3.9 | 0.9 到 2.4 |
— ? |
— ? |
1.3 到 3.5 | 1.3 到 1.9 |
— ? |
±0.8 | 36.5 |
?
輸入和輸出耦合:交流或直流
需要交流耦合還是直流耦合對差分ADC驅動器的選擇有很大的影響。 輸入和輸出耦合之間的考慮因素也不同
交流耦合型輸入級電路見圖11。
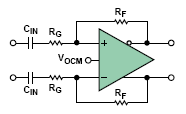
圖11 :交流耦合型ADC驅動器。
對于采用交流耦合輸入的差分至差分應用來說,放大器輸入端呈現的直流共模電壓等于直流輸出共模電壓,因為直流反饋電流被 輸入電容隔離了。 另外,直流反饋系數也是匹配的,完全等于單位1。 VOCM—和由此得到的直流輸入共模電壓—經常被設置在電源電壓 的一半左右。 具有中心型輸入共模范圍的ADC驅動器非常適合這類應用,它們的輸入共模電壓接近規定范圍的中心。
交流耦合單端至差分應用與對應的差分輸入應用非常相似,但在放大器輸入端具有共模紋波—按比例縮小的輸入信號"復制品"。 具 有中心型輸入共模范圍的ADC驅動器將平均輸入共模電壓設定在規定范圍的中間,因而能為大多數應用中的紋波提供足夠的富余度。
當輸入耦合方式可選時,值得人們注意的是,采用交流耦合輸入的ADC驅動器比采用直流耦合輸入的相似驅動器耗散更少的功率,因 為兩個反饋環路中都不存在直流共模電流。
當ADC要求輸入共模電壓與驅動器輸出端電壓完全不同時,交流耦合ADC驅動器的輸出就非常有用。 當VOCM值被設在電源電壓一半附 近時,驅動器將有最大的輸出擺幅,但當驅動要求非常低輸入共模電壓的低電壓ADC時會出現問題。 走出這個困境的簡單方法(圖12)是驅動器輸出和ADC 輸入之間采用交流耦合連接,從驅動器輸出中去除ADC的直流共模電壓,并允許適合ADC的共模電平應用于交流耦合側。 例如,驅動器可以工作在單5V 電源和 VOCM = 2.5V,條件下,而ADC可以工作在單1.8V電源,此時在標記為ADC CMV的點必需施加0.9V的輸入共模電壓。
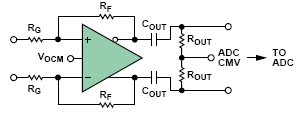
圖 12:采用交流耦合輸出的直流耦合輸入電路
具有偏移型輸入共模范圍的驅動器一般最適合工作在單電源直流耦合系統中,這是因為輸出共模電壓通過反饋環路實現了分壓,而且它 的可變分量可以非常接近地,即負電壓軌。 當采用單端輸入時,輸入共模電壓由于輸入相關的紋波而更接近負電壓軌
采用雙電源、單端或差分輸入以及交流或直流耦合的系統通常可以采用任一種輸入級電路,因為富余度增加了。
表2總結了在輸入耦合和電源的各種組合方式下最常用的ADC驅動器輸入級電路類型。 然而,這些選擇未必總是最好的,應該對每個系統進行具體分析。
表2:耦合和輸入級電路選項
?
| 輸入耦合方式 | 輸入信號 | 電源 | 輸入類型 |
| 任意 | 任意 |
雙電源 ? |
中心型 |
| 交流耦合 |
單端 ? |
單電源 | 中心型 |
| 直流耦合 | 單端 |
單電源 ? |
偏移型 |
|
交流耦合 ? |
差分 ? |
單電源 ? |
中心型 |
|
直流耦合 ? |
差分 ? |
單電源 ? |
中心型 |
?
輸出擺幅
為了最大化ADC的動態范圍,應該將它驅動到滿輸入范圍。 但需要注意:將ADC驅動得太厲害可能有損輸入電路,而驅動不夠的話又會降 低分辨率。 將ADC驅動到滿輸入范圍并不意味著放大器輸出幅度必須達到最大。 差分輸出的一個主要好處是每個輸出幅度只需達到傳 統單端輸出的一半。 驅動器輸出可以遠離電源軌,從而減少失真。 不過對單端驅動器來說沒有這個好處。 當驅動器輸出電壓接近電壓軌時,放大器將損失線性度,并引入失真。
對于對每一毫伏的輸出電壓都有要求的應用來說,表1顯示相當多的ADC驅動器能夠提供軌到軌輸出,其典型富余量從幾毫伏到幾百毫伏不等,具體取決于負載
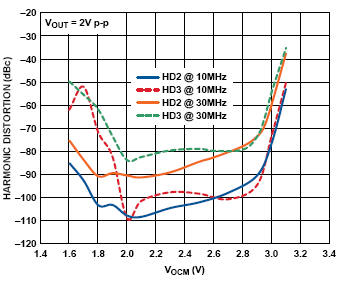
圖 13:采用5V電源的ADA4932在各種頻率下的諧波失真與VOCM的關系。
圖13是 ADA4932在各種頻率下的諧波失真與 VOCM的關系圖,是典型輸出擺幅在每個軌1.2V內(富余量確定的。 輸出擺幅是信號的VOCM與V峰之和(1V )。 值得注意的是,失真在2.8V 以上(3.8 V峰或5V往下1.2V)開始迅速增加。 在低端,失真在2.2V (-1 V峰)時仍很低。 同樣的現象還將出現在帶寬和壓擺率的討論中。
噪聲
ADC的非理想特性包括量化噪聲、電子或隨機噪聲和諧波失真。 在大多數應用中重要的一點是,噪聲通常是寬帶系統中最重要的性能指標。
所有ADC內部都存在量化噪聲,并且取決于位數n,n越大量化噪聲就越小。 因為即使"理想"轉換器也有量化 噪聲,因此量化噪聲可以用作比較隨機噪聲和諧波失真的基準。 ADC驅動器的輸出噪聲應該接近或低于ADC的隨機噪聲和失真。 下面先討論 ADC噪聲和失真的特征,然后介紹如何衡量ADC驅動器噪聲與ADC性能之間的關系。
量化噪聲產生的原因是ADC將具有無限分辨率的模擬信號量化成有限數量的離散值。 n位ADC有2n個二進制值。 兩個相鄰值之間的差代 表了可以分辨的最小差值,這個差值被稱為量化等級的最低有效位(L S B),或q。 因此一個量化等級等于轉換器量程的1/2n。 如果一個不 斷變化的電壓經過一個完美的n位ADC轉換,然后轉換回模擬信號,再從ADC輸入中減去這個信號,那么差值看起來就像噪聲。 它有一個 公式21計算所得有效值(rms):
?
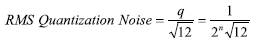 |
??? | (21) |
?
從這里可以得出n位ADC在其奈奎斯待帶寬上的信號與量化噪聲比的對數(dB)公式22,這也是n位轉換器所能取得的最佳信噪比(SNR)。
ADC中的隨機噪聲 包含了熱噪聲、散粒噪聲和閃爍噪聲,一般要大于量化噪聲。 由于ADC的非線性產生的 諧波失真會在輸出信號中產生 與輸入信號諧波有關的有害信號。 總的諧波失真和噪聲 (THD + N)是一個重要的ADC性能參數,它衡量了電子噪聲和諧波失真與接近ADC滿 量程輸入范圍的模擬輸入信號之間的關系。 電子噪聲積分的帶寬包括了所要考慮的最后一個諧波頻率。 THD中的"T"(ttotal,總和)包括了前五個諧波失真分量,是連同噪聲一起的和的平方根,見公式23。
?
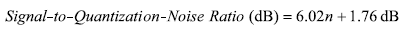 |
??? | (22) |
| ? |
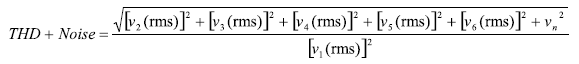
| ? | ??? | (23) |
?
公式23中的v1是輸入信號,在2到在6是前五個諧波失真分量, 在n是ADC的電子噪聲。
T HD+噪聲)的倒數被稱為信號與噪聲失真比,簡稱SINAD,通常用dB表示,見公式24。
?
| ? |
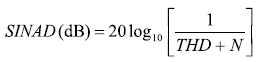
| ? | ??? | (24) |
?
如果SINAD被信號與量化噪聲比代替(公式22),我們就能定義轉換器具有的有效位數(ENOB),前提是這個轉換器的信號與量化噪聲比與SINAD相同(公式25)。
?
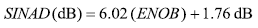 |
??? | (25) |
?
ENOB也能用SINAD項表達,見公式26。
?
| ? |
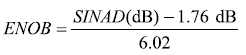
| ? | ??? | (26) |
?
ENOB可以用來比較ADC驅動器的噪聲性能和ADC的噪聲性能,進而判斷是否適合驅動這個ADC。 圖14是一個差分ADC噪聲模型。
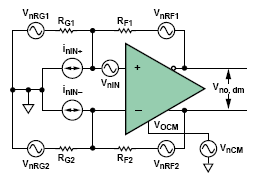
圖 14:差分ADC驅動器的噪聲模型
公式27表明了通常情況下當 β1= b2 ≡ β時,八個噪聲源中每個源對總輸出噪聲密度的貢獻。
?
| ? |
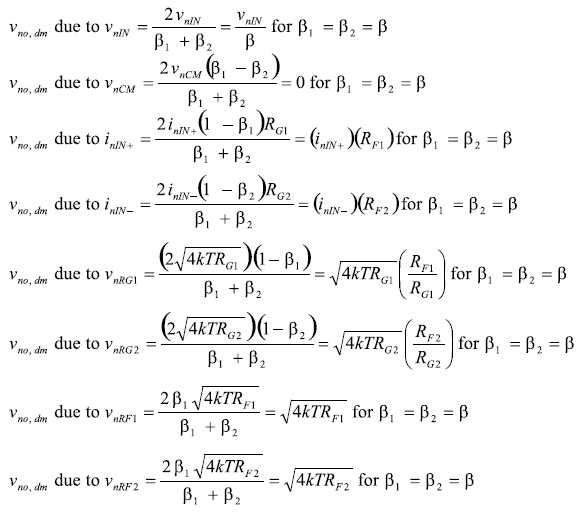
| ? | ??? | (27) |
?
總輸出噪聲電壓密度v不,分米是通過計算這些分量的和平方根得到的。 將這些公式輸入電子表格是計算總輸出噪聲電壓密度的最好方式。 ADI公司網站上還新推出了ADI差分放大器計算器(參考文獻3),用它能快速計算噪聲、增益和差分ADC驅動器的其它參數值。
現在可以將ADC驅動器的噪聲性能與ADC的ENOB作一比較。 描述這一過程的例子是為采用5V電源工作的 AD9445 ADC選擇和評估一款增益為2、2V 滿量程輸入的差分驅動器。 它能處理用一個單極點濾波器限制、占用50M H z(-3d B)帶寬的直接耦合寬帶信號。 從數據手冊中記載的各種條件下的 ENOB參數列表中可以發現:對應50MHz的奈奎斯特帶寬,ENOB=12位。
ADA4939 是一款能夠被直接耦合的高性能寬帶差分ADC驅動器。 在 噪聲性能方面它是驅動AD9445的合適產品嗎? A DA4939數據手冊針對近似為2的差分增益推薦的RF=402Ω、RG=200?,數據手冊給出的 這種情況下的總輸出電壓噪聲密度為9.7nV/Hz。
首先計算給定恒定輸入噪聲功率譜密度下的系統噪聲帶寬BN,它是輸出與決定系統帶寬的實際濾波器相同噪聲功率的等效矩形低通濾波器的帶寬。 對于一個單極濾波,BN等于π/2乘以3dB帶寬,如公式28所示。
?
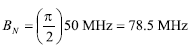 |
??? | (28) |
?
然后在系統帶寬的平方根內對噪聲密度進行積分,得到輸出噪聲有效值(公式29)。
?
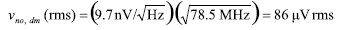 |
??? | (29) |
?
假定噪聲幅度呈高斯分布,那么峰峰值噪聲的計算可以使用常見的±3σ門限(在99.7%的時間內噪聲電壓擺幅位于這些門限之間),見公式30:
?
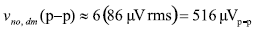 |
??? | (30) |
?
現在可以在12位ENOB、2V滿量程輸入范圍基礎上對驅動器的峰峰輸出噪聲和AD9445 LSB的1 LSB電壓進行比較,其中LSB的計算見公式31。
?
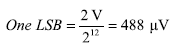 |
??? | (31) |
?
相對于12位ENOB,驅動器的峰峰輸出噪聲與ADC的LSB具有可比性。 因此從噪聲角度看,A DA4939驅動器非常適合這種應用。 最終還必須通過搭建和測試驅動器/ADC組合作出決定。
電源電壓
考慮電源電壓和電流是縮小ADC驅動器選擇范圍的快速途徑。 表1提供了不同電源電壓下ADC驅動器性能的快速查找表。 電源電壓會影響帶寬、信號擺幅和ICMVR 。 衡量這些指標并進行反復權衡對差分放大器的選擇而言至關重要。
電源抑制 (PSR)是另外一個重要的參數。 作為放大器輸入的電源引腳的作用經常被人忽視。 電源線上或耦合進電源線的任何噪聲對輸出信號都有潛在的破壞作用。
考慮ADA4937-1的電源線上存在60MHz、50mVp-p的噪聲這樣一個例子。 它的PSR在50MHz時是-70dB,這意味著電源線上的噪聲在放大器 輸出端將被減少到約16μV。 在1V滿量程輸入的16位系統中,1 LSB是15.3μV,因此電源線上的這個噪聲將"淹沒"LSB。
這種情況可以通過增加串聯表貼鐵氧體磁珠L1/ L 2和并聯旁路電容C1/C2(圖15)加以改進。
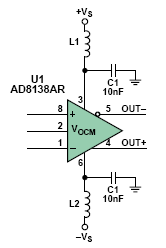
圖 15:電源旁路電路
在50MHz時,磁珠的阻抗是60?,10nF(0.01μF)電容的阻抗是0.32?,由這兩種元件組成的衰減器可以提供45.5dB的衰減(公式32)
?
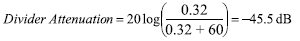 |
??? | (32) |
?
上述分壓式衰減加上-70d B的PSR總共可提供115d B的抑制效果,因而可將噪聲減小到遠低于1 LSB的90nVp-p左右。
諧波失真
頻域中的低諧波失真在窄帶和寬帶系統中都很重要。 驅動器中的非線性會在放大器輸出端產生單頻諧波失真和多頻互調失真。
在噪聲分析例子中使用的方法可以同樣應用于失真分析,即對ADA4939的諧波失真與2V滿量程輸出時AD 94 45 12位ENOB的1 LSB進行比較。 一個ENOB LSB在噪聲分析中代表488μV。
ADA4939規格表中的失真數據為增益為2,比較2德·和 3RD各種頻率的諧波。表3顯示了增益為2和差分輸出擺幅為2 V p-p時的諧波失真數據。
表3:ADA4939的二次和三次諧波失真
?
| 參數 | 諧波失真 |
| HD2 @ 10兆赫 | –102 分貝 |
| HD2 @ 70兆赫 | –83 分貝 |
| HD2 @ 70兆赫 |
–83 分貝 ? |
| HD2 @ 100兆赫 | –77 分貝 |
| HD2 @ 10兆赫 | –101 分貝 |
|
HD2 @ 70兆赫 ? |
–97 分貝 |
|
HD2 @ 100兆赫 ? |
–97 分貝 |
?
這些數據表明,諧波失真隨頻率增加而增加,并且在感興趣帶寬(50M Hz)內二次諧波失真要比三次諧波失真糟糕。 在比感興趣頻率更 高的頻率點的諧波失真值較高,因此它們的幅度可能被系統頻帶限制功能所降低。 如果系統有一個50MHz的磚墻式濾波器,那么就只需要考慮超過25MHz 的頻率點,因為更高頻率的所有諧波將被濾波器濾除。 盡管如此,我們還是要評估頻率最高為50MHz的系統,因為目 前的所有濾波器對諧波的抑制可能都不夠,失真分量可能混疊回信號帶寬內。 圖16給出了ADA4939在各種電源電壓和2Vp-p輸出時的諧波失真與頻率的關系。
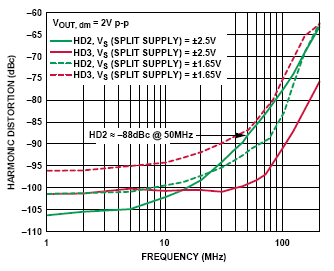
圖 16:諧波失真與頻率的關系
50MHz時的二次諧波失真相對于2Vp-p輸入信號來說大約是-88dBc。 為了比較諧波失真水平和1 ENOB LSB,這個諧波失真值必須被轉換成電壓值,如公式33所示。
?
| ? |
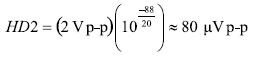
| ? | ??? | (33) |
?
這個失真值只有80μVp-p,或1 ENOB LSB的16%。 因此,從失真的角度看,可以認為ADA4939是AD9445 ADC驅動器的很好選擇。
由于ADC驅動器是負反饋放大器,輸出失真取決于放大器電路中的環路增益值。 負反饋放大器固有的開環失真將被減少 1/(1+L G)倍,其中LG代表可用環路增益。
放大器的輸入(誤差電壓)被乘以一個大的前向電壓增益A(s),然后通過反饋系數β傳送到輸入端,再通過調整輸出使誤差最小。 這樣, 這類放大器的環路增益為A(s)×β。 隨著環路增益(A(s), β或兩者)的降低,諧波失真將增加。 電壓反饋放大器,如積分器,被設計在直流 和低頻率處具有大的A(s),然后隨著1/f在規定高頻點趨向于1而發生滾降。 隨著A(s)的滾降,環路增益下降,失真增加。 因此諧波失真參數是A(s)的倒數。
電流反饋放大器將誤差電流用作反饋信號。 誤差電流被乘以一個大的前向互阻T(s)而轉換成輸出電壓,然后通過反饋系數 1/R F將輸出電壓轉換成反饋電流,以便使輸入誤差電流最小。 因此理想的電流反 饋放大器的環路增益是 T(s) × (1/RF) = T(s)/RF。 同 A(s)一樣, T(s)也有一個 大的直流值,并隨著頻率的增加而滾降,從而降低環路增益,增加諧波失真。
環路增益還直接取決于反饋系數1/RF。 理想電流反饋放大器的環路增益并不取決于閉環電壓增益,因此諧波性能不會隨著閉環增益 的增加而下降。 在實際的電流反饋放大器中,環路增益確實某種程度上取決于閉環增益,但不會達到電壓反饋放大器中那樣的程度。 因此對于高閉環增益和低失真的應用來說,電流反饋放大器,比如 ADA4927, 是比電壓反饋放大器更好的選擇。 從圖17可以看出隨著閉環增益的增加失真性能保持得有多好。
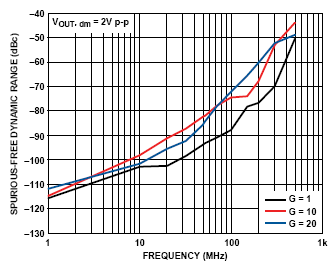
圖 17:失真與頻率和增益的關系
帶寬和壓擺率
帶寬和壓擺率在ADC驅動器應用中特別重要。 一般情況下,器件的帶寬是指小信號帶寬,而壓擺率衡量的是大信號擺幅時放大器輸出端的最大變化率。
EUBW(有效可用帶寬) , 一 個類似于ENOB(有效位數)的首字母縮略詞,用于描述帶寬。 許多ADC驅動器和運放自稱有很寬的帶寬指標, 但并不是所有帶寬都是可用的。 例如,-3dB帶寬是測量帶寬的一種傳統方法,但它并不意味著所有帶寬是可用的。 -3dB帶寬的幅度和 相位誤差的使用比實際"截止"頻率要早十年。 那么什么是放大器的EUBW? 如何確定它的大小? 確定可用帶寬的一個極好方法是查詢數據手冊上的失真圖。
圖18表明,為了使二次和三次諧波保持大于-80dBc,這個ADC驅動器不應用于超過60MHz的頻率。 由于每個應用都不盡相同,系統要求將 成為具有足夠帶寬和足夠失真性能的合適驅動器的選擇準則。
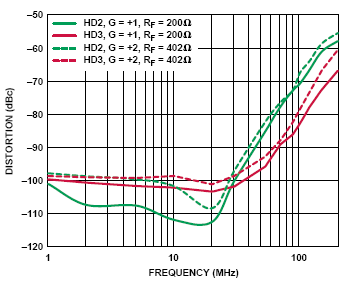
圖 18:ADA4937電流反饋型ADC驅動器的失真曲線
壓擺率,一種大信號參數,指的是放大器輸出在沒有過高失真的情況下能夠跟蹤輸入的最大變化率。 以壓擺率考慮正弦波輸出
?
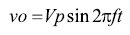 |
??? | (34) |
?
公式34在過零點的導數(變化率)即最大變化率,它等于:
?
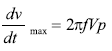 |
??? | (35) |
?
其中 dv/dt max是壓擺率,Vp是峰值電壓,f等于滿功率帶寬(FPBW)。 推算FPBW:
?
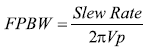 |
??? | (36) |
?
因此,在選擇ADC驅動器時,重點要考慮增益、帶寬和壓擺率(FPBW),以確定放大器是否足夠滿足應用要求。
穩定性
關于差分ADC驅動器的穩定性考慮與運放是一樣的,關鍵參數是相位余量。 雖然特定放大器配置的相位余量可以從數據手冊中獲取, 但在實際系統中由于PCB版圖中的寄生效應這個相位余量會有顯著降低。
負電壓反饋放大器的穩定性取決于其環路增益的大小和符號, A(s) × β. 差分ADC驅動器要比典型的運放電路稍微復雜一點,因為它 有兩個反饋系數。 在公式7和公式8的分母中可以見到環路增益。 公式37提供了在反饋系數不匹配(β1≠ b2)情況下的環路增益。
?
| ? |
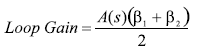
| ? | ??? | (37) |
?
當反饋系數不匹配時,有效反饋系數是兩個反饋系數的簡單平均值。 當它們匹配并被定義為β時,環路增益可以簡化為 A(s) × β.
要想使反饋放大器穩定,其環路增益不允許等于-1(相當于相位偏移-180°、幅度為1)。 對于電壓反饋放大器來說,其開環增益頻率圖上環路增益 值等于1(即0dB)的點正是A(s)值等于反饋系數倒數的地方。 對于基本的放大器應用,反饋是純阻性的,在反饋環路中不會引入 相位偏移。 在反饋系數匹配的情況下,與頻率無關的反饋系數倒數 1 + RF/RG通常被稱為噪聲增益。 如果將以 dB為單位的恒定噪聲增益與開環增益A(s)繪制在同一張圖上,那么兩條曲線的交叉點就是環路增益為1或0dB的地方。 在這個頻率點的A(s) 相位與-180°之間的差值被定義為相位余量。 為了穩定工作,這個相位余量應大于或等于45°。 圖19給出了 RF/RG = 1 (噪聲增益 =2)時A DA4932的單位環路增益點和相位余量。
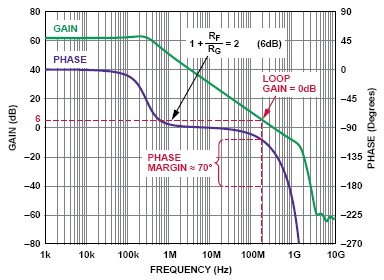
圖19:ADA4932開環增益幅度和相位與頻率的關系
進一步觀察圖19可以發現,A DA4932在噪聲增益為1(每個環路中100%反饋)時有約50°的相位余量。 雖然讓ADC驅動器工作在零增益有點不切實際,但這一結果表明,A DA4932可以穩定工作在小數差分增益(如RF/RG=0.25,噪聲增益=1.25 )。 并不是所有差 分ADC驅動器都能這樣。 最小穩定增益可以在所有ADC驅動器的數據手冊中找到。
電流反饋ADC驅動器的相位增益同樣可以從開環響應中判斷。 電流反饋放大器不再使用前向增益A(s),而是 使 用前向互阻T(s),并 將誤 差電流用作反饋信號。 帶匹配反饋電阻的電流反饋驅動器的環路增益等于T(s)/RF,因此電流反饋放大器環路增益幅度在T(s)=RF時等于1(即0dB)。 這個點在開環互阻和相位圖上很容易找到,定位方法與電壓反饋放大器相同。 注意,繪制電阻與1k?的比值能使阻值表示在對數圖上。 圖20給出了RF=300時A DA4927電流反饋差分ADC驅動器的單位環路增益點和相位余量。
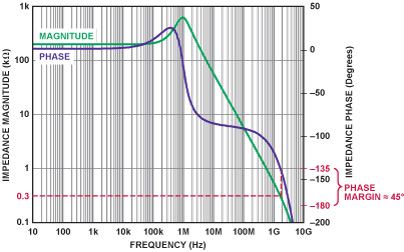
圖20:ADA4927開環增益幅度和相位與頻率的關系
300 ?反饋電阻水平線與互阻幅度曲線的交叉點是環路增益為0dB的地方。 在 這個頻率點,T(s)的相位接近-13 5°,因此 有45°的相位余量。 相位余量和穩定性隨RF的增加而增加,隨RF的減小而減小。 電流反饋放大器應始終使用具有足夠相位余量的純電阻反饋
PCB版圖
在穩定的ADC驅動器設計好后,還必須在PCB上實現。 由于電路板存在寄生成分,總是會損失一些相位余量,因此電路板的寄生效應必 須保持最小,其中特別要關注的是負載電容、反饋環路電感和求和節點電容。 每種寄生電抗都會給反饋環路增加遲滯性相位偏移,從而減小相位余量。 由于 PCB版圖設計不良可能導致20°以上的相位余量損失。
在使用電壓反饋放大器時最好使用盡可能小的RF,以便最小化由 RF和求和節點電容組成的極點引起的相位偏移。 如果要求使用大的RF,寄生電容可以用跨接每個反饋電阻的小電容CF進行補償,對CF的要求是RFCF等于RG乘以求和節點電容。
PCB版圖是設計中最后的必要步驟之一。 遺憾的是,它也是設計中最容易被忽視的步驟之一,即使性能高度依賴于版圖設計的高速電路 也是如此。 馬虎或拙劣的版圖設計可能降低一個高性能設計的性能,甚至使它不能工作。 雖然本文無法涵蓋正確高速PCB 設計的所有方面,但還是要介紹一些關鍵點。
寄生成分將損害高速電路的性能。 寄生電容是由元器件的焊盤、走線、地平面或電源平面引起的。 沒有地平面的長走線將形成寄生電 感,進而導致瞬態響應中的振鈴和其它不穩定現象。 寄生電容在放大器的求和節點處特別危險,因為它會在反饋響應中引入一個極點, 造成尖峰和不穩定。 一種解決方案是確保ADC驅動器安裝和反饋元件焊盤下方區域的所有電路板層都是干凈的地和電源平面。
要使有害寄生電抗最小,首先要使所有走線盡可能短。 RF-4印制板的外層50?走線產生的寄生參數大約為2.8p F/英寸和7n H/英寸。 內層50?走線的寄生電抗將在此基礎上增加約30%。 還要確保在長走線下方有地平面,以使走線電感最小。 保持短小的走線有助于減小寄生電容和寄生電感—并保持設計的完整性。
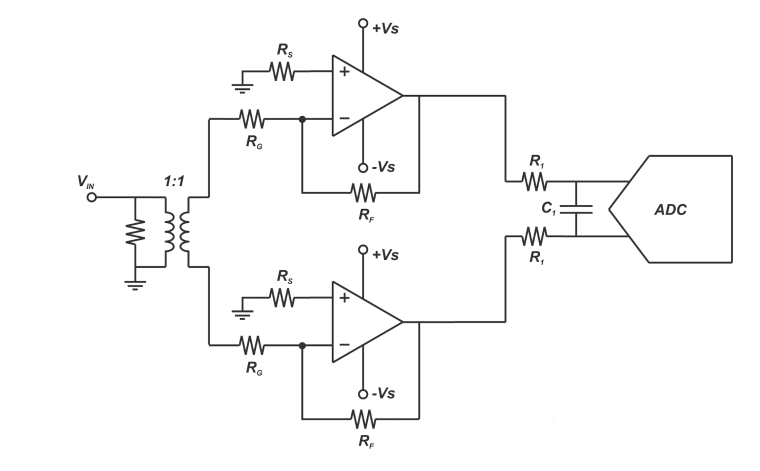
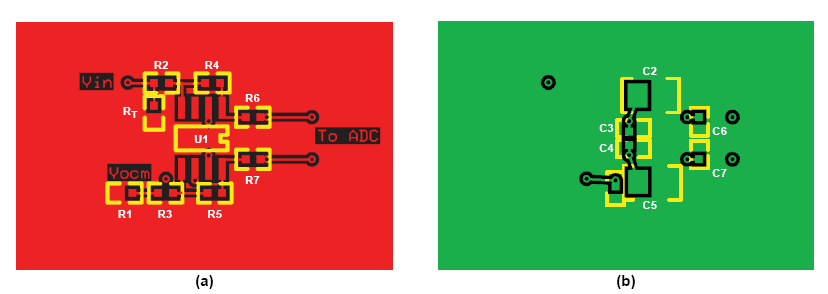
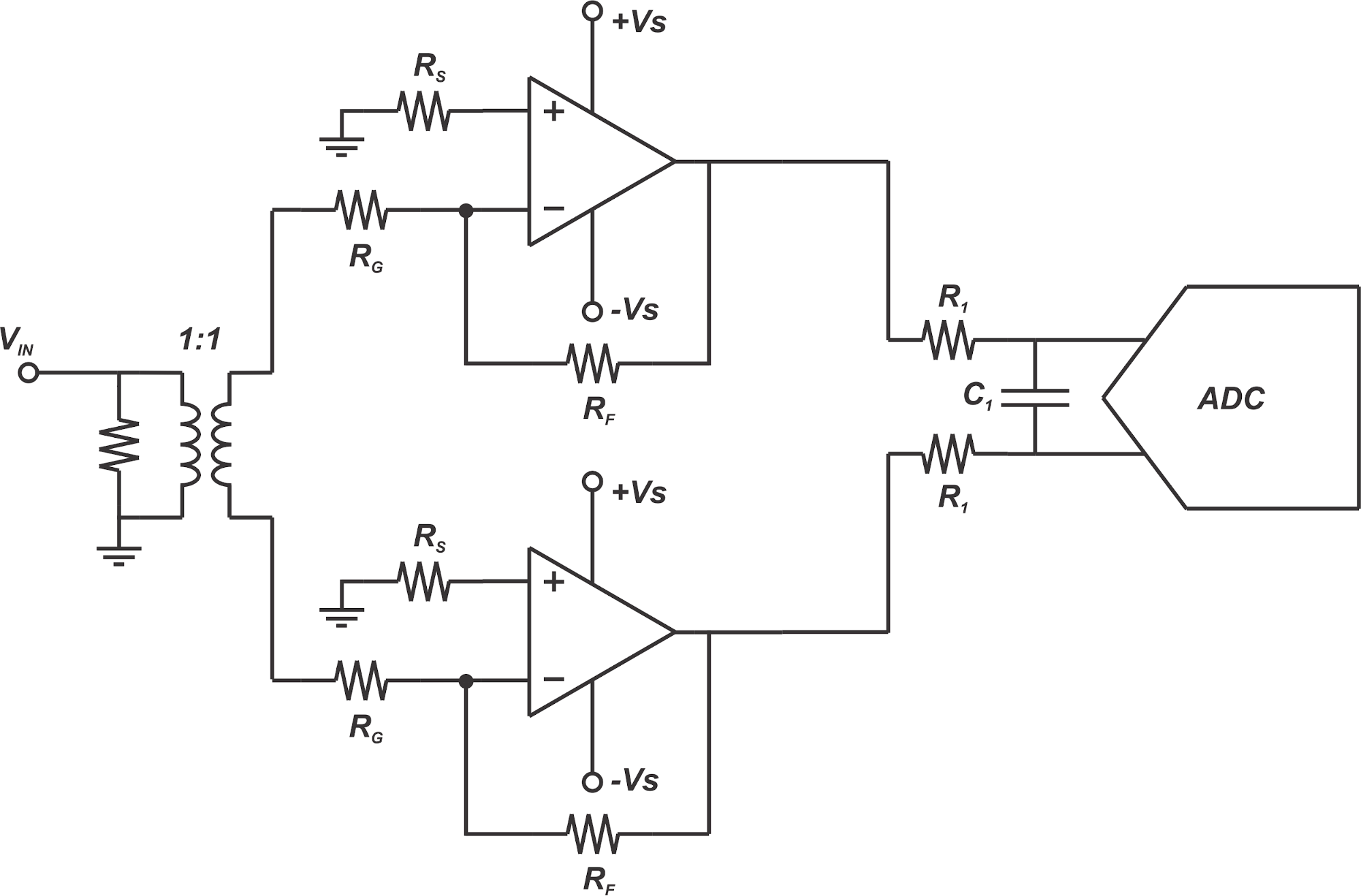
電源旁路是版圖設計中另一個重要的考慮因素。 確保電源旁路電容和VOCM旁路電容盡可能靠近放大器引腳放置。 另外,在電源上使用 多個旁路電容有助于確保為寬帶噪聲提供低阻抗路徑。 圖21給出了一個帶旁路和輸出低通濾波器的典型差分放大器原理圖。 低通濾波 器用于限制進入ADC的帶寬和噪聲。 理想情況下,電源旁路電容回路靠近負載回路,這有助于減小地平面中的環流,從而改善ADC驅動 器性能(圖22a和圖22b)。
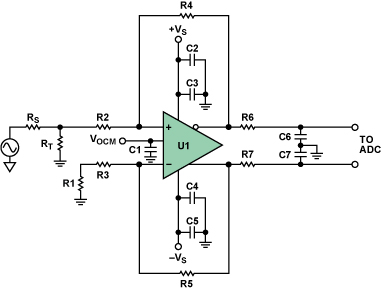
圖21 :帶電源旁路電路和輸出低通濾波器的ADC驅動器
使用地平面和一般的接地技巧是一個具體而復雜的課題,不在本文討論的范圍之內。 不過有幾個要點需要指出,見圖22a和圖22b。 首先,只在一個點將模擬和數字地連接在一起,記住只是單點接地。 這樣做可以使地平面中模擬和數字電流的交互作用最小,而這種交互最終將導致系統中產生"噪聲"。 另外,要將模擬電源終接到模擬電源 平面,數字電源終接到數字電源平面。 對于混合信號IC,要將模擬回路終接到模擬地平面,將數字地回路終接到數字地平面。
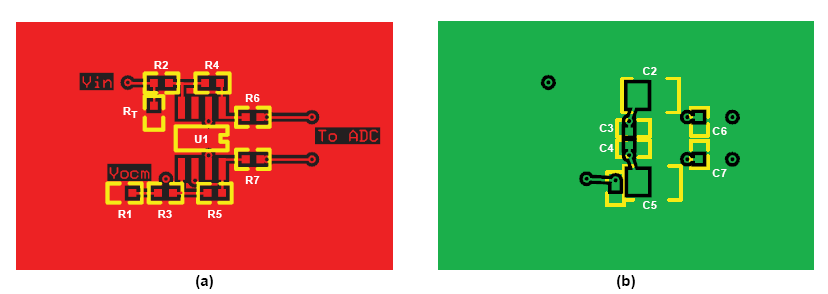
圖23:混合信號的接地方式
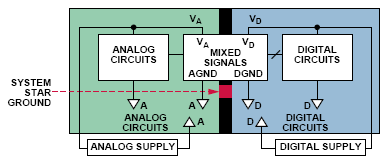
圖 23.混合信號接地。
我們希望當您用ADC驅動器進行設計時這里提供的材料有助于您更加全面地考慮眾多必要因素。 理解差分放大器—并在項目開始時就留意ADC驅動器設計的細節—將使設計過程中發生的問題最少,并使您遠離ADC驅動器故障。
審核編輯:郭婷
 電子發燒友App
電子發燒友App






















評論