文氏橋電路是一個非常經典的電路,歷經多年,盡管存在一些缺點,但仍然是教科書里面的必講內容。從電路結構來看,并不復雜,但是這里面隱含的知識點卻很多,涉及的內容也比較廣泛,有信號與系統的知識,還要用到一點復變函數的知識,還涉及到相位的概念。因此,值得把這個電路仔細研究一下。
知識鋪墊
?什么是文氏橋振蕩?
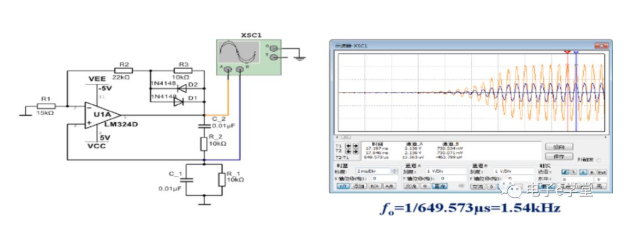
圖1
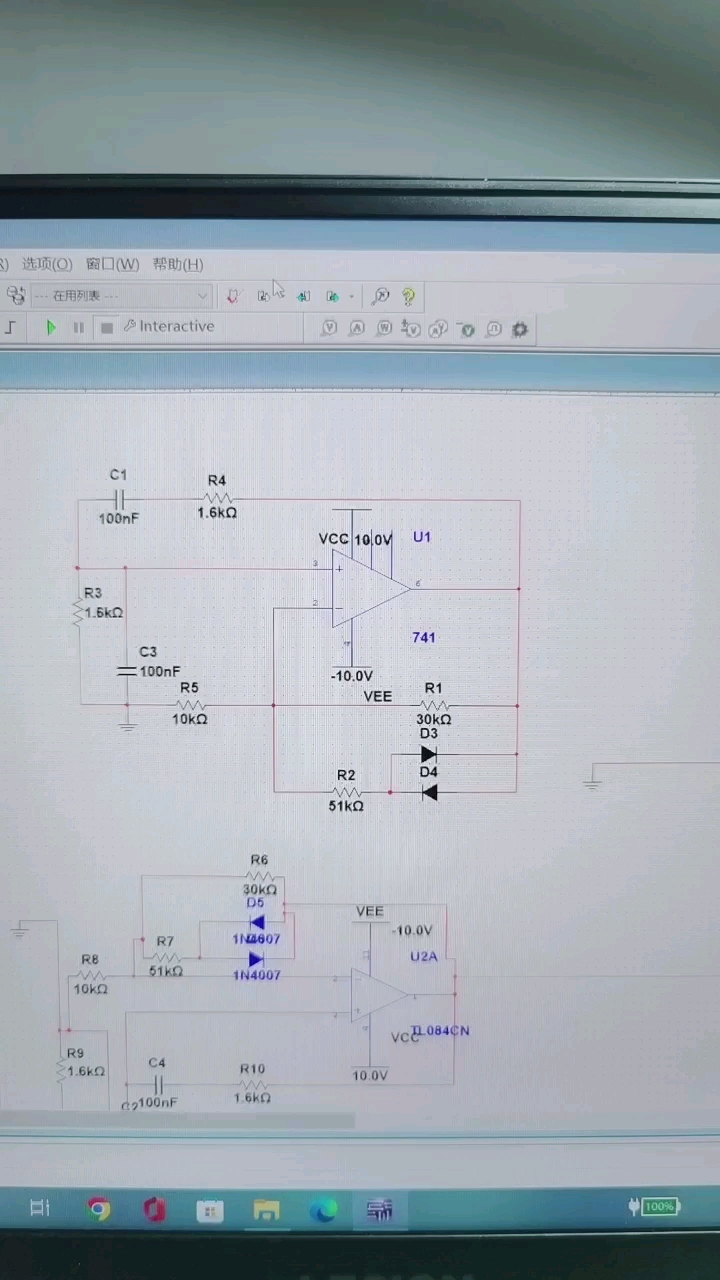
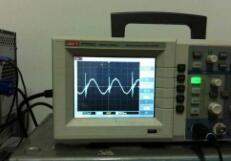
如圖1所示,左邊是文氏橋的電路連接形式,右邊是仿真的結果,從示波器顯示的結果,發現一個1.54KHz的正弦信號從無到有,就這么神奇的產生了,而且信號增大到一定幅值自動穩定下來。
我們都知道,能量是守恒的,不可能憑空產生一個信號,而這個電路沒有任何輸入的信號源,那這個正弦信號的能量來自哪里呢?答案是運放的供電電源。那這個電路之所以會產生這個信號,是由于自激振蕩的結果。
?怎樣才能讓運放電路發生自激振蕩呢?
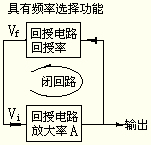
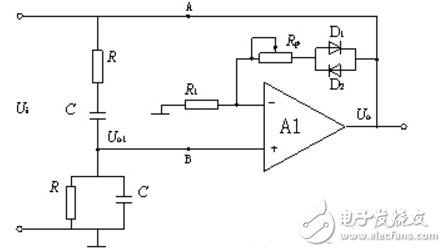
一個閉環的反饋系統可以按照下面的結構圖來描述,如圖2所示。
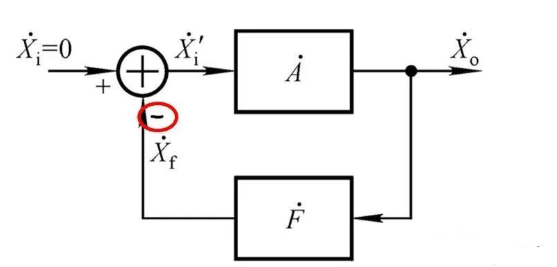
圖2
A可以理解為正向通路系統函數,F為反饋通路系統函數,Xi為輸入量。按照圖2中所畫,實際上引入的是負反饋,所以Xi’=Xi-Xf,Xo=AFXo。
我們知道,交流信號需要用幅值和相位才能描述全面,那要想實現一個信號的自激, 需要同時滿足幅值和相位條件:
幅值條件。 |AF|略》1,因為即使是1.00001,無數個1.00001相乘最終也會是無窮大。
相位條件。 一個信號從原點出發經過系統(A、F)走一圈,再回到原點時,要保持和原來的信號相位一致,正弦信號的周期是360°;對于一個負反饋系統而言,由于負反饋本身就有180°的相位移動,所以需要附加±180°相移,才能使得信號與源信號同相。
而對于正反饋系統,只要不引入額外的相移,就可以保持和原信號同相。
還有一個隱含條件是Xi如果是0,那0放大多少倍都是0,無法自激。因此,系統中我們需要在一開始給入一個初始信號,無論這個信號有多小,終究會放大出一個幅值客觀的信號。
進入正題
我們先看這個文氏橋振蕩電路的下半部分(圖3),從輸出端反饋回來的信號接在的運放的同相端,實際上引入的是正反饋,也就是說只要保持在反饋回路中不引入額外的相移就可以了。
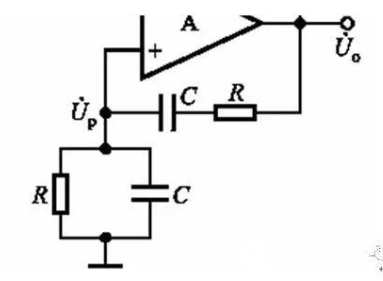
圖3
但是在這個反饋回路當中,有電容的存在。我們都知道,電容實際上會貢獻復數里面的虛部,一旦引入電容,不可避免的要引入相移,那這個正反饋的電路在這里是起到什么作用呢?
先把電路提取出來,整理一下,看的更清楚,如4所示。
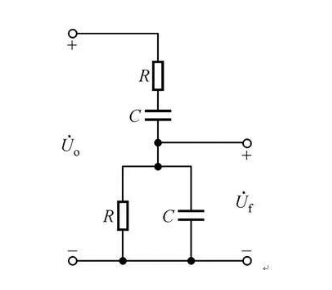
圖4
對這個電路仿真一下,得到下面的幅頻特性曲線(圖5)。不難看出這是一個帶通濾波電路,再由于2個R和2個C的取值一致,所以這是一個單頻點的選頻器,中心頻率是1/(2πRC)。而帶通濾波一定是由高通濾波和低通濾波組成,低通濾波使得信號的相位發生滯后,高通濾波使得信號相位超前;且由于R、C相同,高通與低通的特征頻率一致,使得這個信號的相位移了2次又回到原點了,所以這里完全是虛驚一場。
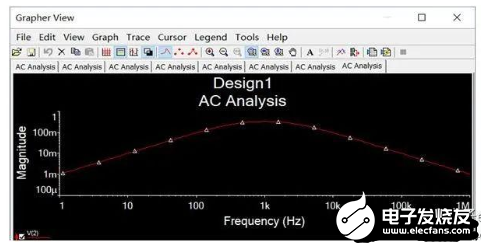
圖5
對于這個正反饋電路我們還得深入剖析,那最最根本的就是傳遞函數了,這里有我們想要的一切信息:
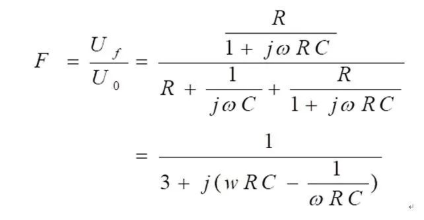
上面這個等式ω為角頻率,這個式子要想取得最大值,需要讓分母的模值最小,也就是分母的虛部為0。
令ωRC-1/(wRC)=0,求得ω=1/RC;再根據ω=2πf,推出f=1/(2πRC)時,整個正反饋電路的模值|F|最大為1/3。
這里其實也解釋了為什么最終輸出的信號頻率是1.54kHz的問題,是根據1/(2πRC)算出來的,也只有這個頻率的信號經過反饋電路時幅值最大,而且沒有相位移動,那你要想改變輸出信號的頻率,就去改R和C的值就好了。
上面我們一直再說的是系統中的F,下面來說A,來看上半部分電路(圖6):
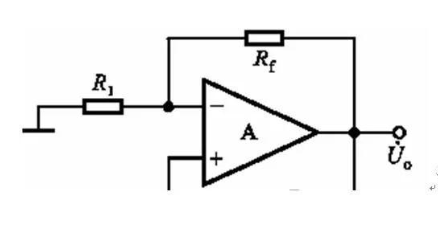
圖6
這個電路我們簡直再熟悉不過了,這就是一個典型的同相放大器,放大倍數為:A=(1+Rf/R1)。
這里Rf與R1是不是隨便取的呢?答案是否定的。因為上文已經知道|F|=1/3;要保證|AF|》=1,|A|必須》=3;根據A=(1+RF/R1),推出(Rf/R1)》=2。
在一開始起振的時候,我們需要讓它Rf略》2R1,當信號達到一定幅度的時候,我們不想讓它繼續增加,需要讓Rf=2R1,因為這個時候|AF|=1,無數個1相乘,最終也是1,所以就穩定下來了。
那問題又來了,怎么能讓這個Rf自動發生變化,從而使得輸出穩定下來呢?
答案是加入穩幅電路,可以在Rf回路上加入2個二極管,也可以用一個負溫度系數的熱敏電阻,隨電流增加,溫度升高,可以自動降低自身阻值。
最后一個問題,就是巧婦難為無米之炊,一開始我們需要把一個小信號給進去,這個小信號還要包含各種頻率成分,才能在眾多信號當中挑選出我們想要的進行自激放大;而在實際電路中,其實很容易獲得,因為在我們的環境中,有各種頻率的噪聲,取之不盡用之不竭,所以這個就不用管了,它自己會進去的。
總 結
所以,一個系統要想實現自激振蕩需要滿足2個條件:

 電子發燒友App
電子發燒友App
























評論