考慮耦合電容及極間電容時的等效電路→分別分析中頻、低頻、高頻時的頻率特性→整個頻率范圍內的頻率特性。
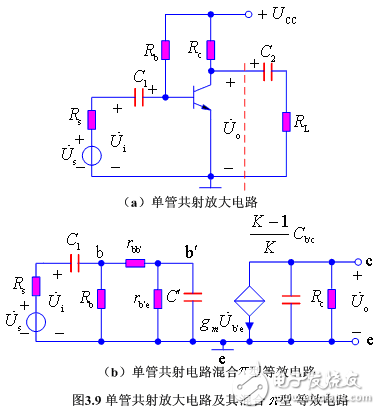
其中, C ‘ = C b’e +( 1?K ) C b‘c 。
下面分別討論中頻、低頻和高頻時地頻率特性。將耦合電容 C 2 和負載電阻 R L 看作是下一級輸入端耦合電容和輸入電阻,暫不考慮。
3.3.1 中頻段
中頻區耦合電容容抗較小,可視為短路,極間電容容抗很大,可視為開路,其混合 π 型等效電路如圖3.10所示。
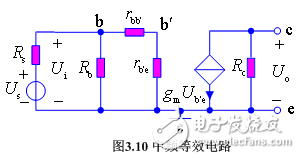
U o =? g m U b’e R c
U b‘e = r b’e r bb‘ + r b’e U i =p U i
U i = r i R s + r i U s
其中, r i = R b //( r bb‘ + r b’e ) , p= r b‘e r bb’ + r b‘e = r b’e r be
∴ U o =? g m p U i R c =? r i R s + r i p g m R c U s
A usm = U o U i =? r i R s + r i p g m R c
將 g m = β r b'e 代入式中 A usm = U o U i =? r i R s + r i p g m R c =? r i R s + r i ???? r b‘e r be g m R c 得
A usm = U o U i =? r i R s + r i p g m R c =? r i R s + r i ???? β R c r be
與用微變等效電路分析的結果一致。
3.3.2 低頻段
低頻區耦合電容容抗較大,其分壓作用較大,不可忽略,極間電容容抗很大,可視為開路,其混合 π 型等效電路如圖3.11所示。
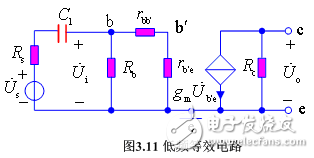
1.確定放大倍數
U ˙ o =? g m U ˙ b’e R c
U ˙ b‘e = r b’e r bb‘ + r b’e U ˙ i =p U ˙ i
U ˙ i = r i R s + r i + 1 jω?? C 1 U ˙ s
∴ U ˙ o =? r i R s + r i + 1 jω?? C 1 p g m R c U ˙ s
變換后得 U ˙ o =? r i R s + r i p g m R c 1 1+ 1 jω??( R s + r i )?? C 1 U ˙ s
∴ A ˙ usL = U ˙ o U ˙ s =? r i R s + r i p g m R c 1 1+ 1 jω??( R s + r i )?? C 1
令 τ L =( R s + r i ) C 1
f L = 1 2π τ L = 1 2π( R s + r i ) C 1
則 A ˙ usL = A usm 1 1+ 1 jω τ L = A usm 1 1?j f L f
幅頻特性 | A ˙ usL |= | A usm | 1+ ( f L f ) 2
相頻特性 ?=? 180 ° +arctan? f L f
當 f= f L 時, | A ˙ usL |= 1 2 A usm , f L 為下限頻率。顯然,下限頻率 f L 主要取決于耦合電容 C 1 所在回路的時間常數 τ L =( R s + r i ) C 1 。

2.確定頻率特性
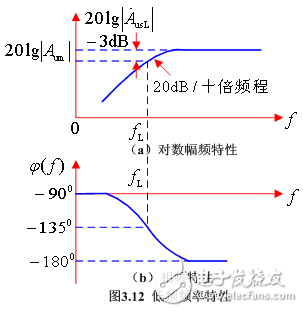
(1)畫對數幅頻特性(波特圖)
將幅頻特性取對數,得
L A =20lg?| A ˙ usL |=20lg?| A usm |?20lg? 1+ ( f L f ) 2
當 f《《 f L 時, L A =20lg?| A usm |?20lg? f L f ,頻率下降十倍 L A 下降20dB;
當 f》》 f L 時, L A ≈20lg?| A usm | , L A 不隨頻率變化;
當 f= f L 時, L A ≈20lg?| A usm |?3dB , L A 比中頻區低3dB。
(2)畫相頻特性
當 f《《0.1 f L 時, ?≈? 90 ° ;
當 f《《10 f L 時, ?≈? 180 ° ;
當 f= f L 時, ?=? 135 ° 。
當 0.1 f L
據此可畫出對數幅頻特性頻率和相頻特性,如圖3.12所示。
3.3.3 高頻段
高頻區耦合電容容抗較小,可視為短路,極間電容容抗很小,不可忽略,其混合 π 型等效電路如圖3.13所示。
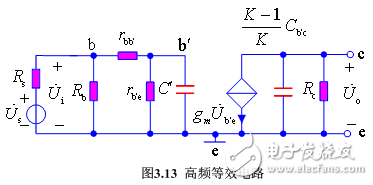
由于 K-1 K C b‘c 所在輸出回路的時間常數比輸入回路 C ′ 的時間常數小得多,故可將 K-1 K C b’c 忽略不計。再利用戴維南定理將輸入回路簡化,則可得高頻簡化等效電路,如圖3.14所示。
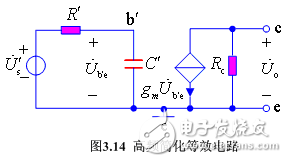
其中 U s ‘ = r i R s + r i ? r b’e r be U ˙ s
R ‘ = r b’e //[ r bb‘ +( R s // R b ) ]
C ′ = C b’e +( 1?K ) C b‘c = C b’e +( 1+ g m R c ) C b‘c
1.確定放大倍數
U ˙ b’e = 1 jω C ‘ R ′ + 1 jω C ’ U ˙ S ‘ = 1 1+jω?R’C‘ U ˙ S ’
而 U ˙ o =? g m U ˙ b‘e R c =? r i R s + r i ? r b’e r be g m R c 1 1+jω? R ‘ C ’ U ˙ s
∴ A ˙ usH = U ˙ o U ˙ s = A usm 1 1+jω? R ′ C ′
令 τ H = R ′ C ′ , f H = 1 2π τ H = 1 2π R ′ C ′
則 A ˙ usH = A usm 1 1+j f f H
幅頻特性 | A ˙ usH |= | A usm | 1+ ( f f H ) 2
相頻特性 ?=? 180 ° ?arctan? f f H
當 f= f H 時, | A ˙ usH |= 1 2 A usm , f H 為上限頻率。顯然,上限頻率 f H 主要取決于電容 C ′ 所在回路的時間常數 τ H = R ′ C ′ 。

2.確定頻率特性
(1)畫對數幅頻特性
將幅頻特性取對數,得
L A =20lg?| A ˙ usH |=20lg?| A usm |?20lg? 1+ ( f f H ) 2
當 f《《 f H 時, L A ≈20lg?| A usm | , L A 不隨頻率變化;
當 f》》 f H 時, L A ≈20lg?| A usm |?20lg?( f f H ) ,頻率增大十倍 L A 下降20dB;
當 f= f L 時, L A ≈20lg?| A usm |?3dB , L A 比中頻區低3dB。
(2)畫相頻特性
當 f《《0.1 f H 時, ?≈? 180 ° ;
當 f》》10 f H 時, ?≈? 270 ° ;
當 f= f L 時, ?=? 225 ° 。
當 0.1 f H
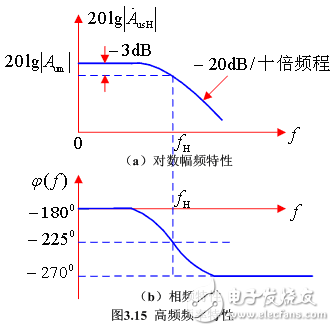
據此可畫出對數幅頻特性頻率和相頻特性,如圖3.15所示。
3.3.4 完整的頻率特性
將中頻、低頻和高頻的放大倍數綜合起來,可得共射放大電路在全頻率范圍內放大倍數的表達式為:
A ˙ = us A usm ( 1?j f L f )( 1+j f f H )
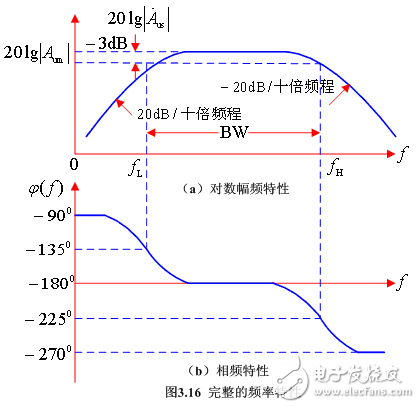
同時,將三段頻率特性綜合起來,即得全頻段頻率特性。如圖3.16所示。
返回頁首
3.4 多級放大電路的頻率響應
授課思路:
多級放大電路總放大倍數→總放大倍數幅頻特性和總相移→多級頻率特性的畫法→幾個結論。
3.4.1 多級放大電路的幅頻特性和相率特性
多級放大電路的總電壓放大倍數為
A ˙ u = A ˙ u1 ? A ˙ u2 ???????????????? A ˙ un
對數幅頻特性 20lg?| A ˙ u |=20lg?| A ˙ u1 |+20lg?| A ˙ u2 |+?+20lg?| A ˙ un |
總相移 ?= ? 1 + ? 2 +?+ ? n

例如,把兩個幅頻特性和相頻特性完全相同的單級放大電路串聯組成一個兩級放大電路,則繪制總幅頻特性和相頻特性時,只需分別將原來單級放大電路的幅頻特性和相頻特性上每一點縱坐標增大一倍即可,如圖3.17所示。
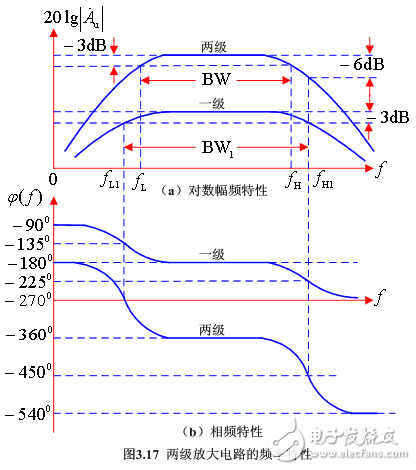
由圖可知
f L 》 f L1 , f H 《 f H1 , BW《 BW 1

3.4.1 多級放大電路的幅頻特性和相率特性
可以證明 1 f H ≈1.1 1 f H1 2 + 1 f H2 2 +?+ 1 f Hn 2
f L =1.1 f L1 2 + f L2 2 +?+ f Ln 2
實際中可以估算,當各級放大電路的時間常數懸殊很大時,可以取起主要作用的那一級作為估算依據。

 電子發燒友App
電子發燒友App












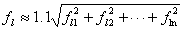
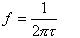













評論